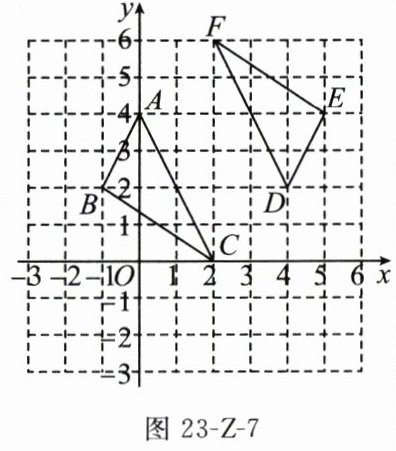
7. 如图 23-Z-7,在平面直角坐标系中,已知 $ \triangle ABC $ 绕一点旋转 $ 180^{\circ} $ 得到 $ \triangle DEF $(点 $ A,B,C $ 的对应点分别是点 $ D,E,F $),则旋转中心的坐标为 ( )
A. $ (3,3) $
B. $ (3,2) $
C. $ (2,3) $
D. $ (2,2) $

A. $ (3,3) $
B. $ (3,2) $
C. $ (2,3) $
D. $ (2,2) $
答案:
C [解析] 将旋转前后的对应点进行连线,如图:
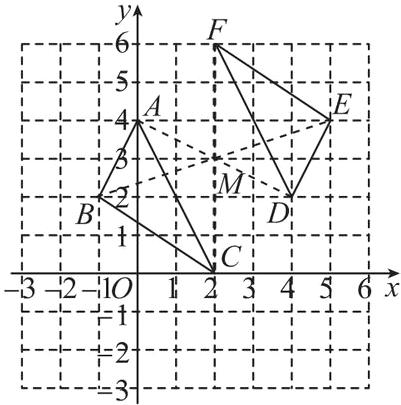
交点 $ M(2,3) $ 即为旋转中心.
故选 C.
C [解析] 将旋转前后的对应点进行连线,如图:

交点 $ M(2,3) $ 即为旋转中心.
故选 C.
8. 如图 23-Z-8,在 $ \triangle AOB $ 中,$ AO=1,BO=AB=\frac{3}{2} $. 将 $ \triangle AOB $ 绕点 $ O $ 按逆时针方向旋转 $ 90^{\circ} $,得到 $ \triangle A^{\prime}OB^{\prime} $,连接 $ AA^{\prime} $,则线段 $ AA^{\prime} $ 的长为 (
A. 1
B. $ \sqrt{2} $
C. $ \frac{3}{2} $
D. $ \frac{3}{2}\sqrt{2} $
B
)A. 1
B. $ \sqrt{2} $
C. $ \frac{3}{2} $
D. $ \frac{3}{2}\sqrt{2} $
答案:
B
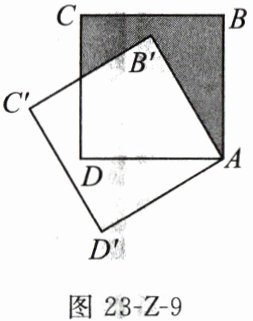
9. 如图 23-Z-9,边长为 1 的正方形 $ ABCD $ 绕点 $ A $ 逆时针旋转 $ 30^{\circ} $ 得到正方形 $ AB^{\prime}C^{\prime}D^{\prime} $,则图中阴影部分的面积为 ( )
A. $ \frac{1}{2} $
B. $ \frac{\sqrt{3}}{3} $
C. $ 1-\frac{\sqrt{3}}{3} $
D. $ 1-\frac{\sqrt{3}}{4} $

A. $ \frac{1}{2} $
B. $ \frac{\sqrt{3}}{3} $
C. $ 1-\frac{\sqrt{3}}{3} $
D. $ 1-\frac{\sqrt{3}}{4} $
答案:
C [解析] 如图,设 $ B'C' $ 与 $ CD $ 的交点为 $ E $,连接 $ AE $.
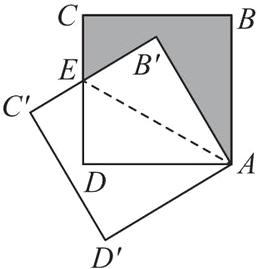
在 $ Rt\triangle AB'E $ 和 $ Rt\triangle ADE $ 中,
$\left\{ \begin{array}{l} AE = AE, \\ AB' = AD, \end{array} \right.$
∴ $ Rt\triangle AB'E \cong Rt\triangle ADE(HL) $,
∴ $ S_{\triangle AB'E} = S_{\triangle ADE} $,$ \angle B'AE = \angle DAE $.
∵旋转角为 $ 30^{\circ} $,
∴ $ \angle DAB' = 60^{\circ} $,
∴ $ \angle DAE = \frac{1}{2}\angle DAB' = \frac{1}{2} × 60^{\circ} = 30^{\circ} $,
∴ $ AE = 2DE $.
在 $ Rt\triangle ADE $ 中,由勾股定理,得 $ DE^{2} + AD^{2} = AE^{2} $,
即 $ DE^{2} + 1 = (2DE)^{2} $,
∴ $ DE = \frac{\sqrt{3}}{3} $,
∴阴影部分的面积 $ = S_{正方形ABCD} - S_{\triangle AB'E} - S_{\triangle ADE} = S_{正方形ABCD} - 2S_{\triangle ADE} = 1 × 1 - 2 × \left( \frac{1}{2} × 1 × \frac{\sqrt{3}}{3} \right) = 1 - \frac{\sqrt{3}}{3} $.
故选 C.
C [解析] 如图,设 $ B'C' $ 与 $ CD $ 的交点为 $ E $,连接 $ AE $.

在 $ Rt\triangle AB'E $ 和 $ Rt\triangle ADE $ 中,
$\left\{ \begin{array}{l} AE = AE, \\ AB' = AD, \end{array} \right.$
∴ $ Rt\triangle AB'E \cong Rt\triangle ADE(HL) $,
∴ $ S_{\triangle AB'E} = S_{\triangle ADE} $,$ \angle B'AE = \angle DAE $.
∵旋转角为 $ 30^{\circ} $,
∴ $ \angle DAB' = 60^{\circ} $,
∴ $ \angle DAE = \frac{1}{2}\angle DAB' = \frac{1}{2} × 60^{\circ} = 30^{\circ} $,
∴ $ AE = 2DE $.
在 $ Rt\triangle ADE $ 中,由勾股定理,得 $ DE^{2} + AD^{2} = AE^{2} $,
即 $ DE^{2} + 1 = (2DE)^{2} $,
∴ $ DE = \frac{\sqrt{3}}{3} $,
∴阴影部分的面积 $ = S_{正方形ABCD} - S_{\triangle AB'E} - S_{\triangle ADE} = S_{正方形ABCD} - 2S_{\triangle ADE} = 1 × 1 - 2 × \left( \frac{1}{2} × 1 × \frac{\sqrt{3}}{3} \right) = 1 - \frac{\sqrt{3}}{3} $.
故选 C.
10. 如图 23-Z-10,在等腰直角三角形 $ ABC $ 中,$ \angle ABC=90^{\circ},BA=BC $,将 $ BC $ 绕点 $ B $ 顺时针旋转 $ \theta(0^{\circ}<\theta<90^{\circ}) $,得到 $ BP $,连接 $ AP,CP $,过点 $ A $ 作 $ AH\perp CP $ 交 $ CP $ 的延长线于点 $ H $,则 $ \angle PAH $ 的度数 (
A. 随着 $ \theta $ 的增大而增大
B. 随着 $ \theta $ 的增大而减小
C. 不变
D. 随着 $ \theta $ 的增大,先增大后减小
C
)A. 随着 $ \theta $ 的增大而增大
B. 随着 $ \theta $ 的增大而减小
C. 不变
D. 随着 $ \theta $ 的增大,先增大后减小
答案:
C [解析]
∵将 $ BC $ 绕点 $ B $ 顺时针旋转 $ \theta(0^{\circ} < \theta < 90^{\circ}) $,得到 $ BP $,
∴ $ BC = BP = BA $,
∴ $ \angle BCP = \angle BPC $,$ \angle BPA = \angle BAP $.
∵ $ \angle ABC + \angle BCP + \angle BPC + \angle BPA + \angle BAP = 360^{\circ} $,$ \angle ABC = 90^{\circ} $,
∴ $ \angle BPC + \angle BPA = 135^{\circ} = \angle CPA $.
∵ $ \angle CPA = \angle AHC + \angle PAH $,
∴ $ \angle PAH = \angle CPA - \angle AHC = 135^{\circ} - 90^{\circ} = 45^{\circ} $,
∴ $ \angle PAH $ 的度数是定值. 故选 C.
∵将 $ BC $ 绕点 $ B $ 顺时针旋转 $ \theta(0^{\circ} < \theta < 90^{\circ}) $,得到 $ BP $,
∴ $ BC = BP = BA $,
∴ $ \angle BCP = \angle BPC $,$ \angle BPA = \angle BAP $.
∵ $ \angle ABC + \angle BCP + \angle BPC + \angle BPA + \angle BAP = 360^{\circ} $,$ \angle ABC = 90^{\circ} $,
∴ $ \angle BPC + \angle BPA = 135^{\circ} = \angle CPA $.
∵ $ \angle CPA = \angle AHC + \angle PAH $,
∴ $ \angle PAH = \angle CPA - \angle AHC = 135^{\circ} - 90^{\circ} = 45^{\circ} $,
∴ $ \angle PAH $ 的度数是定值. 故选 C.
11. 如图 23-Z-11,该图形绕着点 $ O $ 旋转能与自身完全重合,则旋转角最小为 $ $
60
$ ^{\circ} $.
答案:
60
12. 若点 $ A(2,a) $ 关于原点的对称点是 $ B(b,-3) $,则 $ ab $ 的值是 $ $
-6
.
答案:
-6
查看更多完整答案,请扫码查看


