9. 已知二次函数$y=-x^{2}+bx+c$的图象如图22-Z-2所示,并有以下结论:①函数图象与$y$轴正半轴相交;②当$x<0$时,$y$随$x$的增大而增大,则坐标系的原点可能是(
A. 点$A$
B. 点$B$
C. 点$C$
D. 点$D$
B
)A. 点$A$
B. 点$B$
C. 点$C$
D. 点$D$
答案:
B
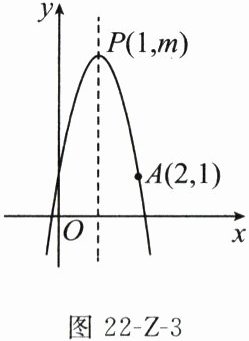
10. 如图22-Z-3,已知二次函数$y=ax^{2}+bx+c$图象的顶点为$P(1,m)$,且经过点$A(2,1)$,有以下结论:①$a<0$;②$abc>0$;③$4a+2b+c=1$;④当$x>1$时,$y$随$x$的增大而减小;⑤对于任意实数$t$,总有$at^{2}+bt≤a+b$.其中正确的有( )
A. 2个
B. 3个
C. 4个
D. 5个
C

A. 2个
B. 3个
C. 4个
D. 5个
答案:
C [解析] ①由抛物线的开口向下,得 $a<0$,故①正确. ② $\because$ 抛物线的顶点为 $P(1, m)$,$\therefore-\frac{b}{2 a}=1$,$\therefore b=-2 a$. $\because a<0$,$\therefore b>0$. $\because$ 抛物线与 $y$ 轴的交点在正半轴上,$\therefore c>0$,$\therefore a b c<0$,故②错误. ③ $\because$ 抛物线经过点 $A(2,1)$,$\therefore 1=a \cdot 2^{2}+2 b+c$,即 $4 a+2 b+c=1$,故③正确. ④由图象可知当 $x>1$ 时,$y$ 随 $x$ 的增大而减小,故④正确. ⑤ $\because$ 抛物线的开口向下,且顶点为 $P(1, m)$,$\therefore$ 当 $x=1$ 时,函数取得最大值 $m$,且 $m=a+b+c$,$\therefore$ 对于任意实数 $t$,总有 $a t^{2}+b t+c \leqslant a+b+c$,$\therefore a t^{2}+b t \leqslant a+b$,故⑤正确. 综上,正确的结论共有 4 个. 故选 C.
11. 若抛物线$y=x^{2}+bx+25$的顶点在$x$轴上,则$b$的值为
$\pm 10$
.
答案:
$\pm 10$
12. 已知二次函数$y=ax^{2}+bx+c$的图象经过点$(0,-3)$,且顶点坐标为$(1,-4)$,则该二次函数的解析式为
$y=x^{2}-2 x-3$
(化为一般形式).
答案:
$y=x^{2}-2 x-3$
13. 二次函数$y=ax^{2}+bx+c$的自变量$x$与函数值$y$的部分对应值如下表:
| $x$ | $\cdots$ | -3 | -2 | -1 | 0 | 1 | $\cdots$ |
| --- | --- | --- | --- | --- | --- | --- | --- |
| $y$ | $\cdots$ | $t$ | $m$ | -2 | -2 | $n$ | $\cdots$ |
则该二次函数图象的对称轴为直线
| $x$ | $\cdots$ | -3 | -2 | -1 | 0 | 1 | $\cdots$ |
| --- | --- | --- | --- | --- | --- | --- | --- |
| $y$ | $\cdots$ | $t$ | $m$ | -2 | -2 | $n$ | $\cdots$ |
则该二次函数图象的对称轴为直线
$x=-\frac{1}{2}$
.
答案:
$x=-\frac{1}{2}$ [解析] $\because$ 当 $x=-1$,$x=0$ 时的函数值相等,$\therefore$ 此函数图象的对称轴为直线 $x=\frac{-1+0}{2}=-\frac{1}{2}$.
14. 将二次函数$y=6x^{2}$的图象先向右平移2个单位长度,再向下平移3个单位长度,得到的图象的函数解析式是
$y=6(x-2)^{2}-3$
.
答案:
$y=6(x-2)^{2}-3$
15. 如图22-Z-4,平行于$x$轴的直线$AC$与函数$y_{1}=x^{2}(x≥0),y_{2}=\frac{1}{3}x^{2}(x≥0)$的图象分别交于$B,C$两点,过点$C$作$y$轴的平行线交$y_{1}$的图象于点$D$,直线$DE// AC$交$y_{2}$的图象于点$E$,则$\frac{DE}{AB}=$
$3-\sqrt{3}$
.
答案:
$3-\sqrt{3}$ [解析] 设点 $A$ 的坐标为 $(0, b)$,则 $B(\sqrt{b}, b)$,$C(\sqrt{3 b}, b)$,$D(\sqrt{3 b}, 3 b)$,$E(3 \sqrt{b}, 3 b)$,$\therefore A B=\sqrt{b}$,$D E=3 \sqrt{b}-\sqrt{3 b}=(3-\sqrt{3}) \sqrt{b}$,$\therefore \frac{D E}{A B}=\frac{(3-\sqrt{3}) \sqrt{b}}{\sqrt{b}}=3-\sqrt{3}$.
查看更多完整答案,请扫码查看


