13. 如图 23-Z-12,在 $ \text{Rt}\triangle ABC $ 中,$ \angle ACB=90^{\circ} $,$ \angle A=60^{\circ},AC=1 $,将 $ \triangle ABC $ 绕点 $ C $ 按逆时针方向旋转得到 $ \triangle A^{\prime}B^{\prime}C $,此时点 $ A^{\prime} $ 恰好落在 $ AB $ 边上,则 $ BB^{\prime} $ 的长为 $
\sqrt{3}
$.
答案:
$ \sqrt{3} $
14. 如图 23-Z-13,点 $ A,B,C $ 的坐标分别为 $ (2,4),(5,2),(3,-1) $. 若以点 $ A,B,C,D $ 为顶点的四边形既是轴对称图形,又是中心对称图形,则点 $ D $ 的坐标为 $
(0,1)
$.
答案:
$ (0,1) $
15. 如图 23-Z-14 所示,将等腰直角三角形 $ ABC $ 绕点 $ A $ 逆时针旋转 $ 15^{\circ} $ 得到 $ \triangle AB^{\prime}C^{\prime} $. 若 $ AC=1 $,则图中阴影部分的面积为 $ $ .
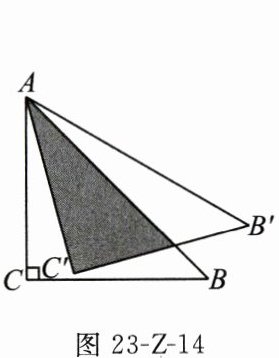

答案:
$ \frac{\sqrt{3}}{6} $ [解析] 如图,设 $ B'C' $ 与 $ AB $ 交于点 $ D $.
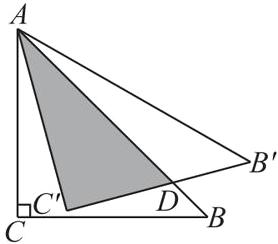
∵ $ \triangle ABC $ 是等腰直角三角形,
∴ $ \angle BAC = 45^{\circ} $.
∵将 $ \triangle ABC $ 绕点 $ A $ 逆时针旋转 $ 15^{\circ} $ 得到 $ \triangle AB'C' $,
∴ $ \angle CAC' = 15^{\circ} $,$ AC' = AC = 1 $,$ \angle C' = \angle C = 90^{\circ} $,
∴ $ \angle C'AD = \angle BAC - \angle CAC' = 45^{\circ} - 15^{\circ} = 30^{\circ} $,
∴ $ AD = 2C'D $.
在 $ Rt\triangle AC'D $ 中,由勾股定理,得 $ AD^{2} = AC'^{2} + C'D^{2} $,
即 $ (2C'D)^{2} = 1^{2} + C'D^{2} $,
解得 $ C'D = \frac{\sqrt{3}}{3} $,
故阴影部分的面积 $ = \frac{1}{2}C'D \cdot AC' = \frac{1}{2} × \frac{\sqrt{3}}{3} × 1 = \frac{\sqrt{3}}{6} $.
$ \frac{\sqrt{3}}{6} $ [解析] 如图,设 $ B'C' $ 与 $ AB $ 交于点 $ D $.

∵ $ \triangle ABC $ 是等腰直角三角形,
∴ $ \angle BAC = 45^{\circ} $.
∵将 $ \triangle ABC $ 绕点 $ A $ 逆时针旋转 $ 15^{\circ} $ 得到 $ \triangle AB'C' $,
∴ $ \angle CAC' = 15^{\circ} $,$ AC' = AC = 1 $,$ \angle C' = \angle C = 90^{\circ} $,
∴ $ \angle C'AD = \angle BAC - \angle CAC' = 45^{\circ} - 15^{\circ} = 30^{\circ} $,
∴ $ AD = 2C'D $.
在 $ Rt\triangle AC'D $ 中,由勾股定理,得 $ AD^{2} = AC'^{2} + C'D^{2} $,
即 $ (2C'D)^{2} = 1^{2} + C'D^{2} $,
解得 $ C'D = \frac{\sqrt{3}}{3} $,
故阴影部分的面积 $ = \frac{1}{2}C'D \cdot AC' = \frac{1}{2} × \frac{\sqrt{3}}{3} × 1 = \frac{\sqrt{3}}{6} $.
16. 如图 23-Z-15,$ P $ 为定角 $ \angle AOB $ 的平分线上的一个定点,且 $ \angle MPN $ 与 $ \angle AOB $ 互补. 若 $ \angle MPN $ 在绕点 $ P $ 旋转的过程中,其两边分别与 $ OA,OB $ 相交于 $ M,N $ 两点,有以下结论:(1)$ PM=PN $ 恒成立;(2)$ OM+ON $ 的值不变;(3)四边形 $ PMON $ 的面积不变. 其中正确的有 $ $ .(填序号)
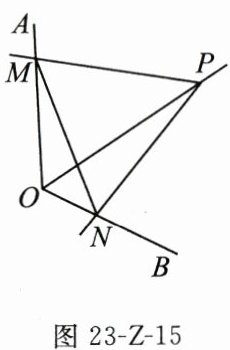

答案:
(1)
(2)
(3) [解析] 如图,过点 $ P $ 分别作 $ PE \perp OA $ 于点 $ E $,$ PF \perp OB $ 于点 $ F $,
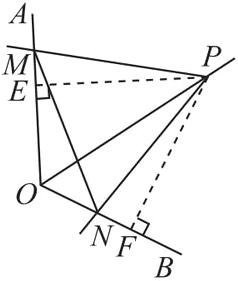
则 $ \angle PEO = \angle PFO = 90^{\circ} $,
∴ $ \angle EPF + \angle AOB = 180^{\circ} $.
又
∵ $ \angle MPN + \angle AOB = 180^{\circ} $,
∴ $ \angle EPF = \angle MPN $,
∴ $ \angle MPE = \angle NPF $.
∵ $ OP $ 平分 $ \angle AOB $,$ PE \perp OA $,$ PF \perp OB $,
∴ $ PE = PF $.
在 $ Rt\triangle POE $ 和 $ Rt\triangle POF $ 中,
$\left\{ \begin{array}{l} OP = OP, \\ PE = PF, \end{array} \right.$
∴ $ Rt\triangle POE \cong Rt\triangle POF(HL) $,
∴ $ OE = OF $.
在 $ \triangle PEM $ 和 $ \triangle PFN $ 中,
$\left\{ \begin{array}{l} \angle MPE = \angle NPF, \\ PE = PF, \\ \angle PEM = \angle PFN = 90^{\circ}, \end{array} \right.$
∴ $ \triangle PEM \cong \triangle PFN(ASA) $,
∴ $ EM = FN $,$ PM = PN $,$ S_{\triangle PEM} = S_{\triangle PFN} $,故
(1)正确;
∴ $ S_{四边形PMON} = S_{四边形PEOF} = $ 定值,故
(3)正确;
$ OM + ON = OE + EM + OF - FN = 2OE = $ 定值,故
(2)正确.
故答案为
(1)
(2)
(3).
(1)
(2)
(3) [解析] 如图,过点 $ P $ 分别作 $ PE \perp OA $ 于点 $ E $,$ PF \perp OB $ 于点 $ F $,

则 $ \angle PEO = \angle PFO = 90^{\circ} $,
∴ $ \angle EPF + \angle AOB = 180^{\circ} $.
又
∵ $ \angle MPN + \angle AOB = 180^{\circ} $,
∴ $ \angle EPF = \angle MPN $,
∴ $ \angle MPE = \angle NPF $.
∵ $ OP $ 平分 $ \angle AOB $,$ PE \perp OA $,$ PF \perp OB $,
∴ $ PE = PF $.
在 $ Rt\triangle POE $ 和 $ Rt\triangle POF $ 中,
$\left\{ \begin{array}{l} OP = OP, \\ PE = PF, \end{array} \right.$
∴ $ Rt\triangle POE \cong Rt\triangle POF(HL) $,
∴ $ OE = OF $.
在 $ \triangle PEM $ 和 $ \triangle PFN $ 中,
$\left\{ \begin{array}{l} \angle MPE = \angle NPF, \\ PE = PF, \\ \angle PEM = \angle PFN = 90^{\circ}, \end{array} \right.$
∴ $ \triangle PEM \cong \triangle PFN(ASA) $,
∴ $ EM = FN $,$ PM = PN $,$ S_{\triangle PEM} = S_{\triangle PFN} $,故
(1)正确;
∴ $ S_{四边形PMON} = S_{四边形PEOF} = $ 定值,故
(3)正确;
$ OM + ON = OE + EM + OF - FN = 2OE = $ 定值,故
(2)正确.
故答案为
(1)
(2)
(3).
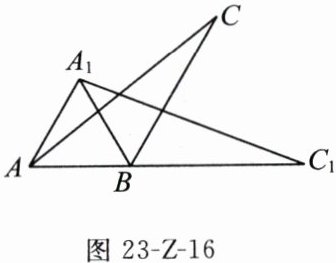
17. (6 分)如图 23-Z-16,将钝角三角形 $ ABC $(其中 $ \angle ABC=120^{\circ} $)绕点 $ B $ 顺时针旋转得到 $ \triangle A_{1}BC_{1} $,使得点 $ C $ 落在 $ AB $ 的延长线上的点 $ C_{1} $ 处,连接 $ AA_{1} $.
(1)写出旋转角的度数;
(2)求证:$ \angle A_{1}AC=\angle C_{1} $.
(1)写出旋转角的度数;
(2)求证:$ \angle A_{1}AC=\angle C_{1} $.

答案:
解:
(1)
∵点 $ C_{1} $ 在 $ AB $ 的延长线上,
∴ $ \angle CBC_{1} = 180^{\circ} - \angle ABC = 180^{\circ} - 120^{\circ} = 60^{\circ} $,
即旋转角的度数为 $ 60^{\circ} $.
(2) 证明:由旋转的性质知 $ \angle A_{1}BC_{1} = \angle ABC = 120^{\circ} $,$ \angle C_{1} = \angle C $,$ A_{1}B = AB $.
∵点 $ A $,$ B $,$ C_{1} $ 在同一直线上,
∴ $ \angle ABA_{1} = 180^{\circ} - \angle A_{1}BC_{1} = 180^{\circ} - 120^{\circ} = 60^{\circ} $,
∴ $ \angle A_{1}BC = \angle ABC - \angle ABA_{1} = 120^{\circ} - 60^{\circ} = 60^{\circ} $.
∵ $ A_{1}B = AB $,$ \angle ABA_{1} = 60^{\circ} $,
∴ $ \triangle ABA_{1} $ 是等边三角形,
∴ $ \angle AA_{1}B = 60^{\circ} = \angle A_{1}BC $,
∴ $ AA_{1} // BC $,
∴ $ \angle A_{1}AC = \angle C $.
又
∵ $ \angle C_{1} = \angle C $,
∴ $ \angle A_{1}AC = \angle C_{1} $.
(1)
∵点 $ C_{1} $ 在 $ AB $ 的延长线上,
∴ $ \angle CBC_{1} = 180^{\circ} - \angle ABC = 180^{\circ} - 120^{\circ} = 60^{\circ} $,
即旋转角的度数为 $ 60^{\circ} $.
(2) 证明:由旋转的性质知 $ \angle A_{1}BC_{1} = \angle ABC = 120^{\circ} $,$ \angle C_{1} = \angle C $,$ A_{1}B = AB $.
∵点 $ A $,$ B $,$ C_{1} $ 在同一直线上,
∴ $ \angle ABA_{1} = 180^{\circ} - \angle A_{1}BC_{1} = 180^{\circ} - 120^{\circ} = 60^{\circ} $,
∴ $ \angle A_{1}BC = \angle ABC - \angle ABA_{1} = 120^{\circ} - 60^{\circ} = 60^{\circ} $.
∵ $ A_{1}B = AB $,$ \angle ABA_{1} = 60^{\circ} $,
∴ $ \triangle ABA_{1} $ 是等边三角形,
∴ $ \angle AA_{1}B = 60^{\circ} = \angle A_{1}BC $,
∴ $ AA_{1} // BC $,
∴ $ \angle A_{1}AC = \angle C $.
又
∵ $ \angle C_{1} = \angle C $,
∴ $ \angle A_{1}AC = \angle C_{1} $.
查看更多完整答案,请扫码查看


