《2025年暑假作业知识出版社八年级理科》

18. 如图,在$□ ABCD$中,$DB= CD,∠C= 70^{\circ},AE⊥BD$于点E.试求$∠DAE$的度数.

$ \because DB = CD $，$ \angle C = 70^{\circ} $，
$ \therefore \angle DBC = \angle C = 70^{\circ} $。
由四边形 $ ABCD $ 是平行四边形，
得 $ AD // BC $，
$ \therefore \angle ADE = \angle DBC = 70^{\circ} $。
又 $ AE \perp BD $，
$ \therefore \angle DAE = 90^{\circ} - \angle ADE = 20^{\circ} $。

答案： $ \because DB = CD $，$ \angle C = 70^{\circ} $，
$ \therefore \angle DBC = \angle C = 70^{\circ} $。
由四边形 $ ABCD $ 是平行四边形，
得 $ AD // BC $，
$ \therefore \angle ADE = \angle DBC = 70^{\circ} $。
又 $ AE \perp BD $，
$ \therefore \angle DAE = 90^{\circ} - \angle ADE = 20^{\circ} $。

19. 如图,在正方形ABCD中,M为AB的中点,$MN⊥MD,BN平分∠CBE$,并交MN于N.求证:$MD= MN$.

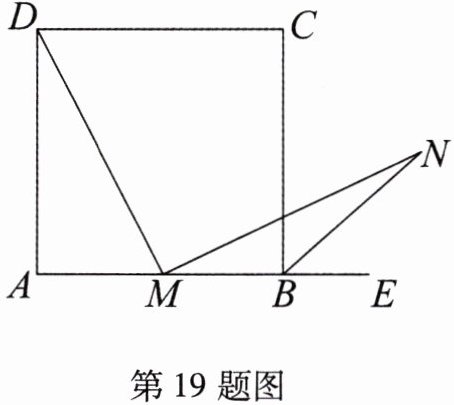
如图，

取 $ AD $ 的中点 $ P $，连接 $ PM $。$ \because M $ 为 $ AB $ 的中点，且四边形 $ ABCD $ 是正方形，
$ \therefore AB = AD $，
$ \therefore AM = AP = BM = PD $，
$ \angle AMP = \angle APM = 45^{\circ} $，
$ \therefore \angle DPM = 135^{\circ} $，
而 $ BN $ 平分 $ \angle CBE $，
$ \therefore \angle NBE = 45^{\circ} $，
$ \therefore \angle MBN = 135^{\circ} $。
$ \because MN \perp MD $，
$ \therefore \angle ADM + \angle AMD = \angle NMB + \angle AMD = 90^{\circ} $，
$ \therefore \angle ADM = \angle NMB $，
即 $ \angle MDP = \angle NMB $。
在 $ \triangle MPD $ 与 $ \triangle NBM $ 中，
$\left\{ \begin{array}{l} \angle DPM = \angle MBN, \\ PD = BM, \\ \angle MDP = \angle NMB, \end{array} \right.$
$ \therefore \triangle MPD \cong \triangle NBM $，
$ \therefore DM = MN $。

答案：
如图，

取 $ AD $ 的中点 $ P $，连接 $ PM $。$ \because M $ 为 $ AB $ 的中点，且四边形 $ ABCD $ 是正方形，
$ \therefore AB = AD $，
$ \therefore AM = AP = BM = PD $，
$ \angle AMP = \angle APM = 45^{\circ} $，
$ \therefore \angle DPM = 135^{\circ} $，
而 $ BN $ 平分 $ \angle CBE $，
$ \therefore \angle NBE = 45^{\circ} $，
$ \therefore \angle MBN = 135^{\circ} $。
$ \because MN \perp MD $，
$ \therefore \angle ADM + \angle AMD = \angle NMB + \angle AMD = 90^{\circ} $，
$ \therefore \angle ADM = \angle NMB $，
即 $ \angle MDP = \angle NMB $。
在 $ \triangle MPD $ 与 $ \triangle NBM $ 中，
$\left\{ \begin{array}{l} \angle DPM = \angle MBN, \\ PD = BM, \\ \angle MDP = \angle NMB, \end{array} \right. $
$ \therefore \triangle MPD \cong \triangle NBM $，
$ \therefore DM = MN $。

20. 如图,在$\triangle ABC$中,$AB= BC,BD平分∠ABC$,四边形ABED是平行四边形,DE交BC于点F,连接CE.求证:四边形BECD是矩形.

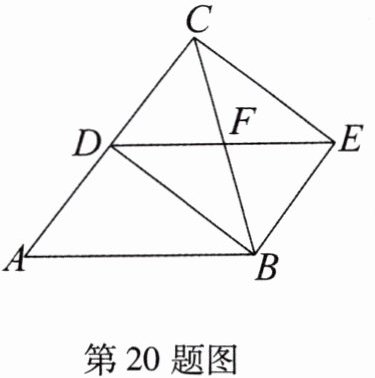
证明：$\because AB = BC $，$ BD $ 平分 $ \angle ABC $，$\therefore BD \perp AC $，$ AD = CD $。$\because $ 四边形 $ ABED $ 是平行四边形，$\therefore BE // AD $，$ BE = AD $，$\therefore BE = CD $，$\therefore $ 四边形 $ BECD $ 是平行四边形。$\because BD \perp AC $，$\therefore \angle BDC = 90^{\circ} $，$\therefore $ 平行四边形 $ BECD $ 是矩形。

答案： $ \because AB = BC $，$ BD $ 平分 $ \angle ABC $，
$ \therefore BD \perp AC $，$ AD = CD $。
$ \because $ 四边形 $ ABED $ 是平行四边形，
$ \therefore BE // AD $，$ BE = AD $，
$ \therefore BE = CD $，
$ \therefore $ 四边形 $ BECD $ 是平行四边形。
$ \because BD \perp AC $，
$ \therefore \angle BDC = 90^{\circ} $，
$ \therefore $ 平行四边形 $ BECD $ 是矩形。