《2025年暑假作业知识出版社八年级理科》

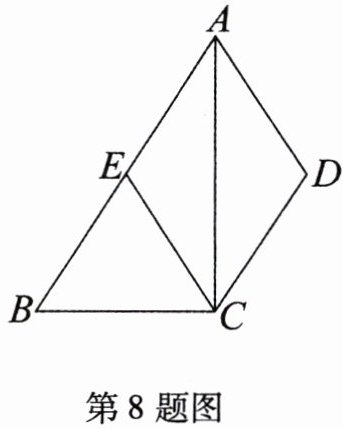
8. 如图,在四边形 ABCD 中,$AB// CD$,AC 平分$∠BAD,CE// AD$交 AB 于 E.
(1)求证:四边形 AECD 是菱形;
∵ AB // CD，即 AE // CD，又 ∵ CE // AD，∴ 四边形 AECD 是平行四边形.∵ AC 平分 ∠BAD，∴ ∠CAE = ∠CAD.又 ∵ AD // CE，∴ ∠ACE = ∠CAD.∴ ∠ACE = ∠CAE.∴ AE = CE.∴ 四边形 AECD 是菱形.
(2)若点 E 是 AB 的中点,试判断$\triangle ABC$的形状,并说明理由.
$\triangle ABC$是直角三角形.理由：解法一：∵ E 是 AB 的中点，∴ AE = BE.又 ∵ AE = CE，∴ BE = CE.∴ ∠B = ∠BCE.∵ ∠B + ∠BCA + ∠BAC = 180°，∴ 2∠BCE + 2∠ACE = 180°.∴ ∠BCE + ∠ACE = 90°，即 ∠ACB = 90°.∴ △ABC 是直角三角形.解法二：连接 DE，则 DE ⊥ AC，且 DE 平分 AC，设 DE 交 AC 于 F.∵ E 是 AB 的中点，∴ EF // BC.∴ BC ⊥ AC，∴ △ABC 是直角三角形.

答案：
(1)
∵ AB // CD，
即 AE // CD，
又
∵ CE // AD，
∴ 四边形 AECD 是平行四边形.
∵ AC 平分 ∠BAD，
∴ ∠CAE = ∠CAD.
又
∵ AD // CE，
∴ ∠ACE = ∠CAD.
∴ ∠ACE = ∠CAE.
∴ AE = CE.
∴ 四边形 AECD 是菱形.
(2) 解法一：
∵ E 是 AB 的中点，
∴ AE = BE.
又
∵ AE = CE，
∴ BE = CE.
∴ ∠B = ∠BCE.
∵ ∠B + ∠BCA + ∠BAC = 180°，
∴ 2∠BCE + 2∠ACE = 180°.
∴ ∠BCE + ∠ACE = 90°.
即 ∠ACB = 90°.
∴ △ABC 是直角三角形.
解法二：连接 DE，则 DE ⊥ AC，且 DE 平分 AC，
设 DE 交 AC 于 F.
∵ E 是 AB 的中点，
∴ EF // BC.
∴ BC ⊥ AC，
∴ △ABC 是直角三角形.

9. 如图,已知直线$y= 2x+3与直线y= -2x-1$.
(1)求两直线与 y 轴的交点 A,B 的坐标; A(0,3)，B(0,-1).
(2)求两直线交点 C 的坐标; C(-1,1).
(3)求$\triangle ABC$的面积. 2.

答案：
(1) A(0, 3)，B(0, -1).
(2) 由 $\begin{cases} y = 2x + 3 \\ y = -2x - 1 \end{cases}$
解得 $\begin{cases} x = -1 \\ y = 1 \end{cases}$.
∴ C(-1, 1).
(3) 2.