2025年教材帮七年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年教材帮七年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1 下列算式中,结果等于$a^{6}$的是( )
A. $a^{4}+a^{2}$
B. $a^{2}+a^{2}+a^{2}$
C. $a^{2}\cdot a^{3}$
D. $a^{2}\cdot a^{2}\cdot a^{2}$
A. $a^{4}+a^{2}$
B. $a^{2}+a^{2}+a^{2}$
C. $a^{2}\cdot a^{3}$
D. $a^{2}\cdot a^{2}\cdot a^{2}$
答案:
D 选项A中不是同类项,不能合并;选项B中合并同类项的结果为3a²;选项C中,a²·a³ = a²⁺³ = a⁵;选项D中,a²·a²·a² = a²⁺²⁺² = a⁶.
2 已知$n$是大于1的自然数,则$(-c)^{n - 1}\cdot(-c)^{n + 1}$等于( )
A. $(-c)^{n^{2}-1}$
B. $-2nc$
C. $-c^{2n}$
D. $c^{2n}$
A. $(-c)^{n^{2}-1}$
B. $-2nc$
C. $-c^{2n}$
D. $c^{2n}$
答案:
D (-c)ⁿ⁻¹·(-c)ⁿ⁺¹ = (-c)ⁿ⁻¹⁺ⁿ⁺¹ = (-c)²ⁿ = c²ⁿ.
3 计算$2^{n}\cdot(-8)\cdot2^{n + 3}$的结果是( )
A. $2^{2n + 6}$
B. $2^{2n + 5}$
C. $-2^{2n + 6}$
D. $-3^{2n + 4}$
A. $2^{2n + 6}$
B. $2^{2n + 5}$
C. $-2^{2n + 6}$
D. $-3^{2n + 4}$
答案:
C 2ⁿ·(-8)·2ⁿ⁺³ = 2ⁿ·(-2³)·2ⁿ⁺³ = -2ⁿ⁺³⁺ⁿ⁺³ = -2²ⁿ⁺⁶.
4 (1)(扬州期中)若$10^{m}=12$,$10^{n}=3$,则$10^{m + n}=$______.
(2)若$a^{m}=2$,$a^{m + n}=10$,则$a^{n}=$______.
(3)(泰州期末)已知$3^{n}\times27 = 3^{8}$,则$n$的值是______.
(2)若$a^{m}=2$,$a^{m + n}=10$,则$a^{n}=$______.
(3)(泰州期末)已知$3^{n}\times27 = 3^{8}$,则$n$的值是______.
答案:
(1)36 因为10ᵐ = 12,10ⁿ = 3,所以10ᵐ⁺ⁿ = 10ᵐ·10ⁿ = 12×3 = 36.
(2)5 因为aᵐ = 2,aᵐ⁺ⁿ = 10,所以aᵐ⁺ⁿ = aᵐ·aⁿ = 2aⁿ = 10. 所以aⁿ = 5.
(3)5 因为3ⁿ×27 = 3ⁿ×3³ = 3ⁿ⁺³,所以3ⁿ⁺³ = 3⁸,所以n + 3 = 8,解得n = 5,所以n的值是5.
(1)36 因为10ᵐ = 12,10ⁿ = 3,所以10ᵐ⁺ⁿ = 10ᵐ·10ⁿ = 12×3 = 36.
(2)5 因为aᵐ = 2,aᵐ⁺ⁿ = 10,所以aᵐ⁺ⁿ = aᵐ·aⁿ = 2aⁿ = 10. 所以aⁿ = 5.
(3)5 因为3ⁿ×27 = 3ⁿ×3³ = 3ⁿ⁺³,所以3ⁿ⁺³ = 3⁸,所以n + 3 = 8,解得n = 5,所以n的值是5.
5 新课标 跨学科 1 kg镭完全衰变后,放出的热量相当于$3.75\times10^{5}$kg煤燃烧放出的热量. 据估计地壳中含有$10^{10}$kg镭,这些镭完全衰变后放出的热量相当于__________kg煤燃烧放出的热量.(结果用科学记数法表示)
答案:
3.75×10¹⁵ 依题意可得3.75×10⁵×10¹⁰ = 3.75×10¹⁵(kg),即10¹⁰ kg镭完全衰变后放出的热量相当于3.75×10¹⁵ kg煤燃烧放出的热量.
6 (易错题)计算:
(1)$(-0.2)^{2024}\times(-\frac{1}{5})^{2025}$;
(2)$(p - q)^{4}\cdot(q - p)^{3}\cdot(p - q)^{2}$;
(3)$x^{n - 1}\cdot x^{n + 3}+x^{2n - 1}\cdot x^{3}$($n$是大于1的正整数).
(1)$(-0.2)^{2024}\times(-\frac{1}{5})^{2025}$;
(2)$(p - q)^{4}\cdot(q - p)^{3}\cdot(p - q)^{2}$;
(3)$x^{n - 1}\cdot x^{n + 3}+x^{2n - 1}\cdot x^{3}$($n$是大于1的正整数).
答案:
解:
(1)原式 = (-$\frac{1}{5}$)²⁰²⁴×(-$\frac{1}{5}$)²⁰²⁵ = (-$\frac{1}{5}$)²⁰²⁴⁺²⁰²⁵ = -($\frac{1}{5}$)⁴⁰⁴⁹.
(2)原式 = (q - p)⁴·(q - p)³·(q - p)² = (q - p)⁴⁺³⁺² = (q - p)⁹.
(3)原式 = xⁿ⁻¹⁺ⁿ⁺³ + x²ⁿ⁻¹⁺³ = x²ⁿ⁺² + x²ⁿ⁺² = 2x²ⁿ⁺².
易错点拨:计算同底数幂的乘法时,一定要先找准底数,再运用同底数幂的乘法的运算性质进行计算,特别要注意符号的变化.
(1)原式 = (-$\frac{1}{5}$)²⁰²⁴×(-$\frac{1}{5}$)²⁰²⁵ = (-$\frac{1}{5}$)²⁰²⁴⁺²⁰²⁵ = -($\frac{1}{5}$)⁴⁰⁴⁹.
(2)原式 = (q - p)⁴·(q - p)³·(q - p)² = (q - p)⁴⁺³⁺² = (q - p)⁹.
(3)原式 = xⁿ⁻¹⁺ⁿ⁺³ + x²ⁿ⁻¹⁺³ = x²ⁿ⁺² + x²ⁿ⁺² = 2x²ⁿ⁺².
易错点拨:计算同底数幂的乘法时,一定要先找准底数,再运用同底数幂的乘法的运算性质进行计算,特别要注意符号的变化.
7 新课标 阅读理解 (淮安期末)如果$x^{n}=y$,那么我们规定$(x,y)=n$. 例如:因为$3^{2}=9$,所以$(3,9)=2$. 记$(m,12)=a$,$(m,8)=b$,$(m,96)=c$,则$a$,$b$和$c$的关系是( )
A. $ab = c$ B. $a^{b}=c$ C. $a + b = c$ D. 无法确定
A. $ab = c$ B. $a^{b}=c$ C. $a + b = c$ D. 无法确定
答案:
C 由题意得,mᵃ = 12,mᵇ = 8,mᶜ = 96. 所以mᵃ·mᵇ = mᶜ. 所以mᵃ⁺ᵇ = mᶜ. 所以a + b = c.
8 (2024·常州武进区校级测试)若$2^{n}+2^{n}+2^{n}+2^{n}=2^{12}$,则$n =$______.
答案:
10 因为2ⁿ + 2ⁿ + 2ⁿ + 2ⁿ = 2¹²,所以4×2ⁿ = 2¹²,则2²×2ⁿ = 2¹²,得2ⁿ⁺² = 2¹²,故有n + 2 = 12,解得n = 10.
9 (易错题)若$a^{m - 2}=3$,$a^{m + 2}=5$,求$a^{2m}$的值.
答案:
解:a²ᵐ = a⁽ᵐ⁻²⁾⁺⁽ᵐ⁺²⁾ = aᵐ⁻²·aᵐ⁺² = 3×5 = 15.
易错点拨:求解本题时易出现a²ᵐ = aᵐ⁻² + aᵐ⁺² = 8的错误,切记aᵐ⁺ⁿ = aᵐ·aⁿ(m,n是正整数).
易错点拨:求解本题时易出现a²ᵐ = aᵐ⁻² + aᵐ⁺² = 8的错误,切记aᵐ⁺ⁿ = aᵐ·aⁿ(m,n是正整数).
10 (新定义题)(镇江期中)规定$a*b = 2^{a}\times2^{b}$.
(1)求$2*3$的值;
(2)若$2*(x + 1)=16$,求$x$的值.
(1)求$2*3$的值;
(2)若$2*(x + 1)=16$,求$x$的值.
答案:
解:
(1)因为a * b = 2ᵃ×2ᵇ,所以2 * 3 = 2²×2³ = 2²⁺³ = 2⁵ = 32.
(2)因为2 * (x + 1) = 16,所以2²×2ˣ⁺¹ = 2⁴,所以2²⁺ˣ⁺¹ = 2⁴,所以2ˣ⁺³ = 2⁴,所以x + 3 = 4,解得x = 1.
(1)因为a * b = 2ᵃ×2ᵇ,所以2 * 3 = 2²×2³ = 2²⁺³ = 2⁵ = 32.
(2)因为2 * (x + 1) = 16,所以2²×2ˣ⁺¹ = 2⁴,所以2²⁺ˣ⁺¹ = 2⁴,所以2ˣ⁺³ = 2⁴,所以x + 3 = 4,解得x = 1.
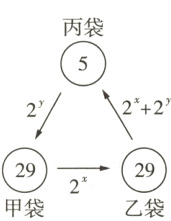
11 (镇江中考)如图,在甲、乙、丙三只袋中分别装有球29个、29个、5个,先从甲袋中取出$2^{x}$个球放入乙袋,再从乙袋中取出$(2^{x}+2^{y})$个球放入丙袋,最后从丙袋中取出$2^{y}$个球放入甲袋,此时三只袋中球的个数都相同,则$2^{x + y}$的值等于( )
A. 128
B. 64
C. 32
D. 16

A. 128
B. 64
C. 32
D. 16
答案:
A 调整后:甲袋中有(29 - 2ˣ + 2ʸ)个球,乙袋中有(29 + 2ˣ - 2ˣ - 2ʸ) = (29 - 2ʸ)个球,丙袋中有(5 + 2ˣ + 2ʸ - 2ʸ) = (5 + 2ˣ)个球. 因为甲、乙、丙三只袋中一共有29 + 29 + 5 = 63(个)球,且调整后三只袋中球的个数相同,所以每只袋中有63÷3 = 21个球,所以5 + 2ˣ = 21,29 - 2ʸ = 21,所以2ˣ = 16,2ʸ = 8,所以2ˣ⁺ʸ = 2ˣ·2ʸ = 16×8 = 128.
查看更多完整答案,请扫码查看


