《2025年教材帮七年级数学下册苏科版》

1（南京期末）下列式子，计算结果为$x^{2}+4x - 21$的是（ ）
A.$(x + 7)(x - 3)$
B.$(x - 7)(x + 3)$
C.$(x + 7)(x + 3)$
D.$(x - 7)(x - 3)$

答案： A 选项 A 中，$(x + 7)(x - 3)=x^{2}+4x - 21$，符合题意；选项 B 中，$(x - 7)(x + 3)=x^{2}-4x - 21$，不符合题意；选项 C 中，$(x + 7)(x + 3)=x^{2}+10x + 21$，不符合题意；选项 D 中，$(x - 7)(x - 3)=x^{2}-10x + 21$，不符合题意.

2（2024·扬州广陵区期末）若$(x^{2}+ax + 2)\cdot(2x - 4)$的结果中不含$x^{2}$项，则$a =$（ ）
A.0
B.2
C.$\frac{1}{2}$
D. - 2

答案： B $(x^{2}+ax + 2)(2x - 4)=2x^{3}-4x^{2}+2ax^{2}-4ax + 4x - 8=2x^{3}+(-4 + 2a)x^{2}+(-4a + 4)x - 8$，因为$(x^{2}+ax + 2)(2x - 4)$的结果中不含$x^{2}$项，所以$-4 + 2a = 0$，解得$a = 2$.

3（南京鼓楼区期末）若$P=(x - 2)(x - 3)$，$Q=(x - 1)(x - 4)$，则$P$与$Q$的大小关系是（ ）
A.$P＞Q$
B.$P＜Q$
C.$P = Q$
D.由$x$的取值而定

答案： A 因为$P - Q=(x - 2)(x - 3)-(x - 1)(x - 4)=(x^{2}-5x + 6)-(x^{2}-5x + 4)=x^{2}-5x + 6 - x^{2}+5x - 4 = 2＞0$，所以$P＞Q$.

4（盐城期中）若$(x - 3)(x + 2)=x^{2}+mx + n$，则$m^{2}n =$______.

答案： -6 因为$(x - 3)(x + 2)=x^{2}-x - 6=x^{2}+mx + n$，所以$m = -1$，$n = -6$，所以$m^{2}n=(-1)^{2}\times(-6)= -6$.

5（镇江期中）将多项式$(x + m)(x - 1)$展开后得到一个关于$x$的二项式，则$m$的值为______.

答案： 0 或 1 $(x + m)(x - 1)=x^{2}-x + mx - m$. 因为$(x + m)(x - 1)$展开后得到一个关于$x$的二项式，当$m = 1$时，原式$=x^{2}-1$，满足条件，当$m = 0$时，原式$=x^{2}-x$，满足条件，所以$m = 0$或$m = 1$.

6（淮安期末）如图，请根据图中所标的数据，计算大长方形的面积. 通过面积不同的计算方法，可以得到的等式是______.

答案： $(3a + 2b)(a + b)=3a^{2}+5ab + 2b^{2}$ 大长方形的长为$3a + 2b$，宽为$a + b$，大长方形的面积可以通过面积公式来表示，即$(3a + 2b)(a + b)$，也可以由三个边长为$a$的正方形，两个边长为$b$的正方形，以及五个长为$b$，宽为$a$的长方形的面积之和来表示，即$3a^{2}+2b^{2}+5ab$，所以$(3a + 2b)(a + b)=3a^{2}+5ab + 2b^{2}$.

7 计算：(1)$(a + 1)(a - 6)-(1 - a)(4 - a)$；
(2)$(2x - y)(4x^{2}+2xy + y^{2})-7y^{3}$.

答案： 解：
(1)原式$=(a^{2}-6a + a - 6)-(4 - a - 4a + a^{2})=a^{2}-5a - 6 - 4 + 5a - a^{2}=-10$.
(2)原式$=8x^{3}+4x^{2}y + 2xy^{2}-4x^{2}y - 2xy^{2}-y^{3}-7y^{3}=8x^{3}-8y^{3}$.

8（宁波中考）先化简，再求值：$(2 + x)(2 - x)+(x - 1)(x + 5)$，其中$x=\frac{3}{2}$.

答案： 解：原式$=4 - 2x + 2x - x^{2}+x^{2}+5x - x - 5 = 4x - 1$，当$x=\frac{3}{2}$时，原式$=4\times\frac{3}{2}-1 = 6 - 1 = 5$.

9（扬州江都区期中）在计算$(2x + a)(x + b)$时，甲错把$b$看成了6，得到的结果是$2x^{2}+8x - 24$；乙错把$a$看成了$-a$，得到的结果是$2x^{2}+14x + 20$.
(1)求$a$，$b$的值；
(2)在(1)的条件下，计算$(2x + a)(x + b)$的结果.

答案： 解：
(1)因为甲错把$b$看成了 6，所以$(2x + a)(x + 6)=2x^{2}+12x + ax + 6a=2x^{2}+(12 + a)x + 6a=2x^{2}+8x - 24$，所以$12 + a = 8$，$6a = -24$，解得$a = -4$；因为乙错把$a$看成了$-a$，所以$(2x - a)(x + b)=2x^{2}+2bx - ax - ab=2x^{2}+(2b - a)x - ab=2x^{2}+14x + 20$，所以$2b - a = 14$，把$a = -4$代入，得$b = 5$，满足$-ab = 20$. 综上，$a = -4$，$b = 5$.
(2)当$a = -4$，$b = 5$时，$(2x + a)(x + b)=(2x - 4)(x + 5)=2x^{2}+10x - 4x - 20=2x^{2}+6x - 20$.

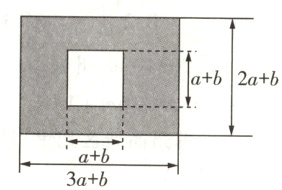
10（2024·连云港期中）如图，某市有一块长为$(3a + b)$米，宽为$(2a + b)$米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像.
(1)求绿化的面积；(用代数式表示)
(2)求出当$a = 3$，$b = 2$时的绿化面积.

答案： 解：
(1)阴影部分的面积$=(3a + b)(2a + b)-(a + b)^{2}=6a^{2}+5ab + b^{2}-a^{2}-2ab - b^{2}=5a^{2}+3ab$，即绿化的面积是$(5a^{2}+3ab)$米$^{2}$.
(2)当$a = 3$，$b = 2$时，绿化面积$=5\times3^{2}+3\times3\times2 = 63$(米$^{2}$).

11 新课标 数学文化 在数学中，为了书写简便，18世纪数学家欧拉使用了求和符号“$\sum$”，如：
$\sum_{k = 1}^{n}k=1 + 2 + 3+\cdots+(n - 1)+n$；
$\sum_{k = 3}^{n}(x + k)=(x + 3)+(x + 4)+\cdots+(x + n)$.
若$\sum_{k = 2}^{n}(x - k)(x - k + 1)=3x^{2}-15x + m$，则$m =$______，$n =$______.

答案： 20 4 由$3x^{2}-15x + m$中二次项的系数为 3 可得，$n = 4$，所以$\sum_{k = 2}^{4}(x - k)(x - k + 1)=(x - 2)(x - 1)+(x - 3)(x - 2)+(x - 4)(x - 3)=x^{2}-3x + 2+x^{2}-5x + 6+x^{2}-7x + 12=3x^{2}-15x + 20=3x^{2}-15x + m$，所以$m = 20$.

12（新定义题）对于任何有理数，我们规定一种运算$\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad - bc$. 例如：$\begin{vmatrix}1&2\\3&4\end{vmatrix}=1\times4 - 2\times3=-2$.
(1)请你按照这个规定计算$\begin{vmatrix}-2&4\\3&5\end{vmatrix}$的值；
(2)请你按照这个规定计算$\begin{vmatrix}a + 1&3a\\a - 2&a - 1\end{vmatrix}$的值，其中$a^{2}-3a + 1 = 0$.

答案： 解：
(1)$\begin{vmatrix}-2&4\\3&5\end{vmatrix}=-2\times5 - 4\times3=-22$.
(2)$\begin{vmatrix}a + 1&3a\\a - 2&a - 1\end{vmatrix}=(a + 1)(a - 1)-3a(a - 2)=a^{2}-a + a - 1 - 3a^{2}+6a=-2a^{2}+6a - 1$. 因为$a^{2}-3a + 1 = 0$，所以$a^{2}-3a=-1$，所以$\begin{vmatrix}a + 1&3a\\a - 2&a - 1\end{vmatrix}=-2(a^{2}-3a)-1=-2\times(-1)-1 = 1$.