2025年教材帮七年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年教材帮七年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
12(扬州邗江区期中改编)已知$(x - 2020)^{2}+(x - 2022)^{2}=48$,则$(x - 2021)^{2}=$______.
答案:
12. 23 设$x - 2021 = a$,则$x - 2020 = a + 1$,$x - 2022 = a - 1$. 因为$(x - 2020)^{2}+(x - 2022)^{2}=48$,所以$(a + 1)^{2}+(a - 1)^{2}=48$,所以$a^{2}+2a + 1+a^{2}-2a + 1 = 48$,所以$2a^{2}+2 = 48$,所以$a^{2}=23$,即$(x - 2021)^{2}=23$.
13 图1是一个长为$4a$,宽为$b$的长方形,沿图中虚线剪开,先把大长方形平均分成四个小长方形,然后用这四个小长方形拼成一个“回”字形正方形,如图2.

(1)图2中阴影部分的面积为______;
(2)观察图2,则$(a + b)^{2},(a - b)^{2},ab$之间的等量关系是______;
(3)根据(2)中的结论,若$x + y = 5,xy=\frac{9}{4}$,则$x - y =$______;
(4)实际上通过计算图形的面积可以探求相应的等式,如图3,可以得到的一个等式是______.

(1)图2中阴影部分的面积为______;
(2)观察图2,则$(a + b)^{2},(a - b)^{2},ab$之间的等量关系是______;
(3)根据(2)中的结论,若$x + y = 5,xy=\frac{9}{4}$,则$x - y =$______;
(4)实际上通过计算图形的面积可以探求相应的等式,如图3,可以得到的一个等式是______.
答案:
13.
(1)$(b - a)^{2}$ 由题图2可知,阴影部分为边长为$b - a$的正方形,所以阴影部分的面积为$(b - a)^{2}$.
(2)$(a + b)^{2}-(a - b)^{2}=4ab$ 由题图2可知,边长为$a + b$的大正方形的面积减去边长为$b - a$的小正方形的面积等于四个长、宽分别为$b$,$a$的小长方形面积的和,所以$(a + b)^{2}-(a - b)^{2}=4ab$.
(3)$\pm4$ 因为$(x + y)^{2}-(x - y)^{2}=4xy$,而$x + y = 5$,$xy=\frac{9}{4}$,所以$5^{2}-(x - y)^{2}=4\times\frac{9}{4}$,所以$(x - y)^{2}=16$,所以$x - y=\pm4$.
(4)$(a + b)(3a + b)=3a^{2}+4ab + b^{2}$ 长为$3a + b$,宽为$a + b$的长方形的面积为$(a + b)(3a + b)$,而该长方形由三个边长为$a$的正方形,四个长、宽分别为$b$,$a$的长方形和一个边长为$b$的正方形组成,所以$(a + b)(3a + b)=3a^{2}+4ab + b^{2}$.
(1)$(b - a)^{2}$ 由题图2可知,阴影部分为边长为$b - a$的正方形,所以阴影部分的面积为$(b - a)^{2}$.
(2)$(a + b)^{2}-(a - b)^{2}=4ab$ 由题图2可知,边长为$a + b$的大正方形的面积减去边长为$b - a$的小正方形的面积等于四个长、宽分别为$b$,$a$的小长方形面积的和,所以$(a + b)^{2}-(a - b)^{2}=4ab$.
(3)$\pm4$ 因为$(x + y)^{2}-(x - y)^{2}=4xy$,而$x + y = 5$,$xy=\frac{9}{4}$,所以$5^{2}-(x - y)^{2}=4\times\frac{9}{4}$,所以$(x - y)^{2}=16$,所以$x - y=\pm4$.
(4)$(a + b)(3a + b)=3a^{2}+4ab + b^{2}$ 长为$3a + b$,宽为$a + b$的长方形的面积为$(a + b)(3a + b)$,而该长方形由三个边长为$a$的正方形,四个长、宽分别为$b$,$a$的长方形和一个边长为$b$的正方形组成,所以$(a + b)(3a + b)=3a^{2}+4ab + b^{2}$.
14 已知$a + b + c = 1,a^{2}+b^{2}+c^{2}=2$,求$ab + bc + ac$的值.
答案:
14. 解:因为$a + b + c = 1$,
所以$(a + b + c)^{2}=a^{2}+b^{2}+c^{2}+2ab + 2bc + 2ac = 1$.
因为$a^{2}+b^{2}+c^{2}=2$,
所以$2 + 2ab + 2bc + 2ac = 1$,
所以$ab + bc + ac=-\frac{1}{2}$,
即$ab + bc + ac$的值为$-\frac{1}{2}$.
所以$(a + b + c)^{2}=a^{2}+b^{2}+c^{2}+2ab + 2bc + 2ac = 1$.
因为$a^{2}+b^{2}+c^{2}=2$,
所以$2 + 2ab + 2bc + 2ac = 1$,
所以$ab + bc + ac=-\frac{1}{2}$,
即$ab + bc + ac$的值为$-\frac{1}{2}$.
15 计算:$(3^{2}+1)\times(3^{4}+1)\times(3^{8}+1)\times\cdots\times(3^{64}+1)\times8 + 1$.
答案:
15. 解:$(3^{2}+1)\times(3^{4}+1)\times(3^{8}+1)\times\cdots\times(3^{64}+1)\times8 + 1$
$=(3^{2}-1)\times(3^{2}+1)\times(3^{4}+1)\times(3^{8}+1)\times\cdots\times(3^{64}+1)+1$
$=(3^{4}-1)\times(3^{4}+1)\times(3^{8}+1)\times\cdots\times(3^{64}+1)+1$
$=(3^{8}-1)\times(3^{8}+1)\times\cdots\times(3^{64}+1)+1$
$=3^{128}-1 + 1$
$=3^{128}$.
$=(3^{2}-1)\times(3^{2}+1)\times(3^{4}+1)\times(3^{8}+1)\times\cdots\times(3^{64}+1)+1$
$=(3^{4}-1)\times(3^{4}+1)\times(3^{8}+1)\times\cdots\times(3^{64}+1)+1$
$=(3^{8}-1)\times(3^{8}+1)\times\cdots\times(3^{64}+1)+1$
$=3^{128}-1 + 1$
$=3^{128}$.
16 观察下列各式:
$1^{2}+(1\times2)^{2}+2^{2}=(1\times2 + 1)^{2}$;
$2^{2}+(2\times3)^{2}+3^{2}=(2\times3 + 1)^{2}$;
$3^{2}+(3\times4)^{2}+4^{2}=(3\times4 + 1)^{2}$;
……
探究以上式子的规律,试写出第$n$($n$为正整数)个式子,并验证其正确性.
$1^{2}+(1\times2)^{2}+2^{2}=(1\times2 + 1)^{2}$;
$2^{2}+(2\times3)^{2}+3^{2}=(2\times3 + 1)^{2}$;
$3^{2}+(3\times4)^{2}+4^{2}=(3\times4 + 1)^{2}$;
……
探究以上式子的规律,试写出第$n$($n$为正整数)个式子,并验证其正确性.
答案:
16. 解:第$n$个式子为$n^{2}+[n(n + 1)]^{2}+(n + 1)^{2}=[n(n + 1)+1]^{2}$.
因为$n^{2}+[n(n + 1)]^{2}+(n + 1)^{2}$
$=n^{2}+(n^{2}+n)^{2}+n^{2}+2n + 1$
$=n^{2}+n^{4}+2n^{3}+n^{2}+n^{2}+2n + 1$
$=n^{4}+2n^{3}+3n^{2}+2n + 1$,
$[n(n + 1)+1]^{2}$
$=[n(n + 1)]^{2}+2n(n + 1)+1$
$=(n^{2}+n)^{2}+2n^{2}+2n + 1$
$=n^{4}+2n^{3}+n^{2}+2n^{2}+2n + 1$
$=n^{4}+2n^{3}+3n^{2}+2n + 1$,
所以$n^{2}+[n(n + 1)]^{2}+(n + 1)^{2}=[n(n + 1)+1]^{2}$.
因为$n^{2}+[n(n + 1)]^{2}+(n + 1)^{2}$
$=n^{2}+(n^{2}+n)^{2}+n^{2}+2n + 1$
$=n^{2}+n^{4}+2n^{3}+n^{2}+n^{2}+2n + 1$
$=n^{4}+2n^{3}+3n^{2}+2n + 1$,
$[n(n + 1)+1]^{2}$
$=[n(n + 1)]^{2}+2n(n + 1)+1$
$=(n^{2}+n)^{2}+2n^{2}+2n + 1$
$=n^{4}+2n^{3}+n^{2}+2n^{2}+2n + 1$
$=n^{4}+2n^{3}+3n^{2}+2n + 1$,
所以$n^{2}+[n(n + 1)]^{2}+(n + 1)^{2}=[n(n + 1)+1]^{2}$.
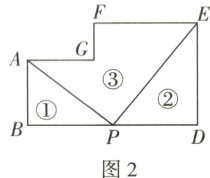
17 两个边长分别为$a,b(a > b)$的正方形如图1放置,现在取$BD$的中点$P$,连接$PA,PE$,如图2,把图形分割成三部分,分别标记为①,②,③,对应图形的面积分别记为$S_{①}$,$S_{②}$,$S_{③}$.
(1)用字母$a,b$分别表示$S_{①}$,$S_{②}$.
(2)若$a - b = 2,ab = 15$,求$S_{①}+S_{②}$.
(3)若$S_{①}+S_{②}=3,ab = 1$,求$S_{③}$.

(1)用字母$a,b$分别表示$S_{①}$,$S_{②}$.
(2)若$a - b = 2,ab = 15$,求$S_{①}+S_{②}$.
(3)若$S_{①}+S_{②}=3,ab = 1$,求$S_{③}$.


答案:
17. 解:由题意得,$AB = b$,$DE = a$,$BP = DP=\frac{1}{2}(a + b)$,
所以$S_{①}=\frac{1}{2}\times\frac{1}{2}(a + b)b=\frac{1}{4}(ab + b^{2})$,
$S_{②}=\frac{1}{2}\times\frac{1}{2}(a + b)a=\frac{1}{4}(a^{2}+ab)$.
(2)由
(1)得,
$S_{①}+S_{②}=\frac{1}{4}(ab + b^{2})+\frac{1}{4}(a^{2}+ab)=\frac{1}{4}(ab + b^{2}+a^{2}+ab)=\frac{1}{4}(a^{2}+2ab + b^{2})=\frac{1}{4}(a + b)^{2}=\frac{1}{4}[(a - b)^{2}+4ab]$,
当$a - b = 2$,$ab = 15$时,
$S_{①}+S_{②}=\frac{1}{4}\times(2^{2}+4\times15)=\frac{1}{4}\times(4 + 60)=16$.
(3)由
(2)知$S_{①}+S_{②}=\frac{1}{4}(a^{2}+2ab + b^{2})$,
因为$S_{①}+S_{②}=3$,$ab = 1$,
所以$\frac{1}{4}(a^{2}+2\times1 + b^{2})=3$,解得$a^{2}+b^{2}=10$,
所以$S_{③}=a^{2}+b^{2}-(S_{①}+S_{②})=10 - 3 = 7$.
所以$S_{①}=\frac{1}{2}\times\frac{1}{2}(a + b)b=\frac{1}{4}(ab + b^{2})$,
$S_{②}=\frac{1}{2}\times\frac{1}{2}(a + b)a=\frac{1}{4}(a^{2}+ab)$.
(2)由
(1)得,
$S_{①}+S_{②}=\frac{1}{4}(ab + b^{2})+\frac{1}{4}(a^{2}+ab)=\frac{1}{4}(ab + b^{2}+a^{2}+ab)=\frac{1}{4}(a^{2}+2ab + b^{2})=\frac{1}{4}(a + b)^{2}=\frac{1}{4}[(a - b)^{2}+4ab]$,
当$a - b = 2$,$ab = 15$时,
$S_{①}+S_{②}=\frac{1}{4}\times(2^{2}+4\times15)=\frac{1}{4}\times(4 + 60)=16$.
(3)由
(2)知$S_{①}+S_{②}=\frac{1}{4}(a^{2}+2ab + b^{2})$,
因为$S_{①}+S_{②}=3$,$ab = 1$,
所以$\frac{1}{4}(a^{2}+2\times1 + b^{2})=3$,解得$a^{2}+b^{2}=10$,
所以$S_{③}=a^{2}+b^{2}-(S_{①}+S_{②})=10 - 3 = 7$.
查看更多完整答案,请扫码查看


