2025年教材帮七年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年教材帮七年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
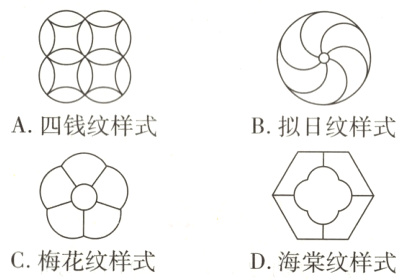
1(知识点1)苏州园林中的花窗图案丰富多样,美不胜收.下列花窗图案中可以由一个基本图案经过平移得到的是 ( )

答案:
1. A
2(知识点1)[新课标 真实情境]在下列实例中,属于平移现象的个数有 ( )
①时针运转;②电梯上升;③火车直线行驶;④地球自转;⑤电视机在传送带上运动.
A. 1个
B. 2个
C. 3个
D. 4个
①时针运转;②电梯上升;③火车直线行驶;④地球自转;⑤电视机在传送带上运动.
A. 1个
B. 2个
C. 3个
D. 4个
答案:
2. C①时针运转,是旋转现象;②电梯上升,是平移现象;③火车直线行驶,是平移现象;④地球自转,是旋转现象;⑤电视机在传送带上运动,是平移现象.故属于平移现象的个数有3个.
3(知识点3)如图,为保持原图案的基本样式,应在空白处补上下列选项中的 ( )


答案:
3. B 观察原图案,每一行的前2个正方形向右平移2格即可得到右侧部分,由此规律可知,题图中空白部分应是第4行前2个正方形向右平移2格后得到的图案.故选B.
4(知识点2)(易错题)如图,在三角形ABC中,BC = 9 cm. 将三角形ABC沿直线MN平移得到三角形DEF,点B的对应点为E. 若平移的距离为2 cm,则CE的长为 ( )
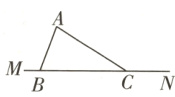
A. 2 cm
B. 7 cm
C. 2 cm或9 cm
D. 7 cm或11 cm

A. 2 cm
B. 7 cm
C. 2 cm或9 cm
D. 7 cm或11 cm
答案:
4. D 由平移的性质可知,$BE = 2$cm.
当三角形ABC沿直线MN向右平移得到三角形DEF时,$CE = BC - BE = 7$cm;
当三角形ABC沿直线MN向左平移得到三角形DEF时,$CE = BC + BE = 11$cm.
所以CE的长为7cm或11cm.
易错点拨:本题易因忽略分类讨论,而导致漏解.
当三角形ABC沿直线MN向右平移得到三角形DEF时,$CE = BC - BE = 7$cm;
当三角形ABC沿直线MN向左平移得到三角形DEF时,$CE = BC + BE = 11$cm.
所以CE的长为7cm或11cm.
易错点拨:本题易因忽略分类讨论,而导致漏解.
5(知识点1)如图所示的4根火柴棒形成象形汉字“口”,平移火柴棒后,“口”字能变成的象形汉字是图中的______.(填序号)


答案:
5. ①
6(知识点2)如图,把梯形ABCD沿AD方向平移得到梯形EFGH,其中∠C = 90°,HG = 24 cm,WG = 8 cm,WC = 6 cm,则阴影部分的面积为______.


答案:
6. $168$cm² 因为梯形ABCD沿AD方向平移得到梯形EFGH,
所以$CD = HG = 24$cm,$\angle G = \angle C = 90^{\circ}$,$S_{梯形ABCD}=S_{梯形EFGH}$,
所以$DW = DC - WC = 24 - 6 = 18$(cm).
因为$S_{阴影部分}+S_{梯形EDWF}=S_{梯形DHGW}+S_{梯形EDWF}$,
所以$S_{阴影部分}=S_{梯形DHGW}=\frac{1}{2}(DW + HG)\times WG=\frac{1}{2}\times(18 + 24)\times 8 = 168$(cm²).
所以$CD = HG = 24$cm,$\angle G = \angle C = 90^{\circ}$,$S_{梯形ABCD}=S_{梯形EFGH}$,
所以$DW = DC - WC = 24 - 6 = 18$(cm).
因为$S_{阴影部分}+S_{梯形EDWF}=S_{梯形DHGW}+S_{梯形EDWF}$,
所以$S_{阴影部分}=S_{梯形DHGW}=\frac{1}{2}(DW + HG)\times WG=\frac{1}{2}\times(18 + 24)\times 8 = 168$(cm²).
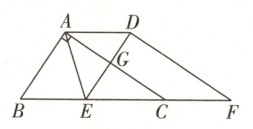
7(知识点2)如图,在直角三角形ABC中,∠BAC = 90°,将三角形ABC沿直线BC向右平移2 cm得到三角形DEF,DE与AC交于点G,连接AD,AE. 给出以下结论:
①AD//BE;②∠B = ∠ADE;③DE⊥AC;④BE = AD.
其中所有正确结论的序号有______.
①AD//BE;②∠B = ∠ADE;③DE⊥AC;④BE = AD.
其中所有正确结论的序号有______.

答案:
7. ①②③④ 因为三角形ABC沿直线BC向右平移2cm得到三角形DEF,
所以$\angle DEF = \angle B$,$AB// DE$,$AD// BE$,$BE = AD$,故①④正确.
因为$AD// BE$,所以$\angle ADE = \angle DEF$,
所以$\angle B = \angle ADE$,故②正确.
因为$\angle BAC = 90^{\circ}$,$AB// DE$,
所以$\angle EGC = \angle BAC = 90^{\circ}$,
所以$DE\perp AC$,故③正确.
所以$\angle DEF = \angle B$,$AB// DE$,$AD// BE$,$BE = AD$,故①④正确.
因为$AD// BE$,所以$\angle ADE = \angle DEF$,
所以$\angle B = \angle ADE$,故②正确.
因为$\angle BAC = 90^{\circ}$,$AB// DE$,
所以$\angle EGC = \angle BAC = 90^{\circ}$,
所以$DE\perp AC$,故③正确.
8 如图是某公园里一处长方形风景欣赏区ABCD,长AB = 60米,宽BC = 24米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为2米,那么小童沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为 ( )

A. 108米
B. 106米
C. 104米
D. 102米

A. 108米
B. 106米
C. 104米
D. 102米
答案:
8. C小童从出口A到出口B所走的路线长为$60+(24 - 2)\times 2 = 104$(米).
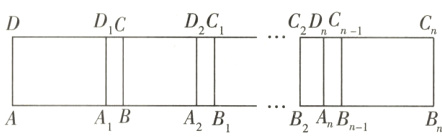
9(规律探究题)如图,在长方形ABCD中,AB = 6,第1次平移将长方形ABCD沿AB的方向平移5个单位长度,得到长方形A₁B₁C₁D₁,第2次平移将长方形A₁B₁C₁D₁沿A₁B₁方向平移5个单位长度,得到长方形A₂B₂C₂D₂,…,第n次平移将长方形Aₙ₋₁Bₙ₋₁Cₙ₋₁Dₙ₋₁沿Aₙ₋₁Bₙ₋₁的方向平移5个单位长度,得到长方形AₙBₙCₙDₙ(n≥2,且n为整数).
(1)求AB₁和AB₂的长;
(2)若ABₙ的长为56,求n的值.
(1)求AB₁和AB₂的长;
(2)若ABₙ的长为56,求n的值.

答案:
9. 解:
(1)由题意,得$AA_{1}=5$,$A_{1}A_{2}=5$,$A_{2}B_{2}=A_{1}B_{1}=AB = 6$,$A_{2}B_{1}=A_{1}B_{1}-A_{1}A_{2}=6 - 5 = 1$,
所以$AB_{1}=AA_{1}+A_{1}A_{2}+A_{2}B_{1}=5 + 5 + 1 = 11$,$AB_{2}=AA_{1}+A_{1}A_{2}+A_{2}B_{2}=5 + 5 + 6 = 16$.
(2)因为$AB_{1}=11 = 2\times 5 + 1$,$AB_{2}=16 = 3\times 5 + 1$,
由此可推出$AB_{n}=(n + 1)\times 5 + 1 = 56$.
解得$n = 10$.
(1)由题意,得$AA_{1}=5$,$A_{1}A_{2}=5$,$A_{2}B_{2}=A_{1}B_{1}=AB = 6$,$A_{2}B_{1}=A_{1}B_{1}-A_{1}A_{2}=6 - 5 = 1$,
所以$AB_{1}=AA_{1}+A_{1}A_{2}+A_{2}B_{1}=5 + 5 + 1 = 11$,$AB_{2}=AA_{1}+A_{1}A_{2}+A_{2}B_{2}=5 + 5 + 6 = 16$.
(2)因为$AB_{1}=11 = 2\times 5 + 1$,$AB_{2}=16 = 3\times 5 + 1$,
由此可推出$AB_{n}=(n + 1)\times 5 + 1 = 56$.
解得$n = 10$.
10 如图,在边长为1个单位长度的正方形网格中,三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′.
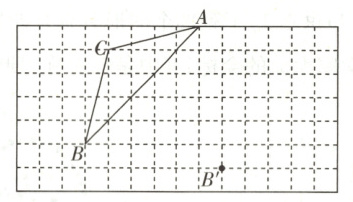
根据下列条件,解答相关的问题:
(1)画出三角形A′B′C′;
(2)连接AA′,CC′,那么AA′与CC′的关系是______,线段AC扫过的图形的面积为______.

根据下列条件,解答相关的问题:
(1)画出三角形A′B′C′;
(2)连接AA′,CC′,那么AA′与CC′的关系是______,线段AC扫过的图形的面积为______.
答案:
10. 解:
(1)如图所示,三角形$A'B'C'$即为所求.

(2)平行且相等 10 提示:如图所示,$AA'$与$CC'$的关系是平行且相等. 线段AC扫过的图形的面积为$10\times 2 - 2\times\frac{1}{2}\times 4\times 1 - 2\times\frac{1}{2}\times 6\times 1 = 10$.
10. 解:
(1)如图所示,三角形$A'B'C'$即为所求.

(2)平行且相等 10 提示:如图所示,$AA'$与$CC'$的关系是平行且相等. 线段AC扫过的图形的面积为$10\times 2 - 2\times\frac{1}{2}\times 4\times 1 - 2\times\frac{1}{2}\times 6\times 1 = 10$.
11 如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动______格.
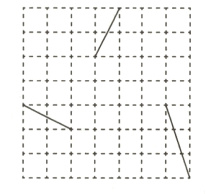

答案:
11. 9 如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形. 根据平移的基本性质知,左边的线段向右平移3格,中间的线段向下平移2格,最右边的线段先向左平移2格,再向上平移2格,此时平移的格数为$3 + 2 + 2 + 2 = 9$,其他平移方法都不少于9格,故至少需要移动9格.

11. 9 如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形. 根据平移的基本性质知,左边的线段向右平移3格,中间的线段向下平移2格,最右边的线段先向左平移2格,再向上平移2格,此时平移的格数为$3 + 2 + 2 + 2 = 9$,其他平移方法都不少于9格,故至少需要移动9格.

查看更多完整答案,请扫码查看


