《2025年教材帮七年级数学下册苏科版》

1 新课标 真实情境 小岩打算购买气球装扮学校“毕业典礼”活动会场，气球的种类有笑脸和爱心两种，两种气球的价格不同，但同一种气球的价格相同. 由于会场布置需要，购买时以一束(4个气球)为单位，已知第一、二束气球的价格如图所示，则第三束气球的价格为（ ）

A.19元
B.18元
C.16元
D.15元

答案： B 设一个笑脸气球的价格为x元，一个爱心气球的价格为y元.
根据题意，得$\begin{cases}3x + y = 16, &①\\x + 3y = 20, &②\end{cases}$
$(① + ②)\div2$，得$2x + 2y = 18$.
所以第三束气球的价格为18元.

2 （牡丹江中考）如图，在长为15，宽为12的长方形中，有形状、大小完全相同的5个小长方形，则图中阴影部分的面积为（ ）

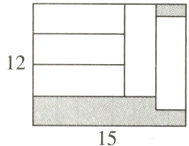
A.35
B.45
C.55
D.65

答案： B 设小长方形的长为x，宽为y.
根据题意，得$\begin{cases}x + 2y = 15,\\x = 3y,\end{cases}$解得$\begin{cases}x = 9,\\y = 3.\end{cases}$
所以$S_{阴影}=15×12 - 5xy = 45$.

3 新课标 数学文化 我国古代问题：以绳测井，若将绳三折测之，绳多四尺，若将绳四折测之，绳多一尺，井深几何？这段话的意思是：用绳子量井深，把绳三折来量，井外余绳四尺，把绳四折来量，井外余绳一尺，井深几尺？则该问题的井深是 ______ 尺.

答案： 8 设绳长为x尺，井深为y尺.
根据题意，得$\begin{cases}\frac{1}{3}x - y = 4, &①\\\frac{1}{4}x - y = 1. &②\end{cases}$
$① - ②$，得$\frac{1}{12}x = 3$，解得$x = 36$.
将$x = 36$代入①，得$y = 8$，所以井深8尺.

4 一个两位数，个位数字与十位数字的和是8，个位数字与十位数字互换后所成的新数比原数小18，则原数是 ______.

答案： 53 设原两位数的十位数字为x，个位数字为y，
根据题意，得$\begin{cases}x + y = 8,\\10x + y - (10y + x) = 18.\end{cases}$
解得$\begin{cases}x = 5,\\y = 3.\end{cases}$
所以$10x + y = 10×5 + 3 = 53$，
所以原两位数为53.

5 新课标 真实情境 （海南中考）2023年5月10日，搭载天舟六号货运飞船的长征七号遥七运载火箭，在我国文昌航天发射场点火发射成功. 为了普及航空航天科普知识，某校组织学生去文昌卫星发射中心参观学习. 已知该校租用甲、乙两种不同型号的客车共15辆，租用1辆甲型客车需600元，1辆乙型客车需500元，租车费共8 000元，问甲、乙两种型号客车各租多少辆？

答案： 解：设租用甲型客车x辆，乙型客车y辆.
根据题意，得$\begin{cases}x + y = 15,\\600x + 500y = 8000.\end{cases}$解得$\begin{cases}x = 5,\\y = 10.\end{cases}$
答：租用甲型客车5辆，乙型客车10辆.

6 （南京期中）南京红山动物园与南京牛首山大约相距30千米，一辆电动车和一辆自行车从两地同时出发相向而行，1小时后相遇. 相遇后，自行车继续前进，电动车没电了，通过路边充电站速充20分钟后，按原路返回，在电动车再次出发15分钟后追上了自行车，这时电动车、自行车从出发到再次相遇各自行了多少千米？

答案： 解：设电动车的速度是x千米/时，自行车的速度是y千米/时，
根据题意得$\begin{cases}(x + y)×1 = 30,\\\frac{20 + 15}{60}y = \frac{15}{60}x,\end{cases}$解得$\begin{cases}x = 21,\\y = 9.\end{cases}$
故电动车行驶的路程是$21×(1 + \frac{15}{60}) = \frac{105}{4}$（千米），
自行车行驶的路程是$9×(1 + \frac{20 + 15}{60}) = \frac{57}{4}$（千米）.
答：电动车从出发到再次相遇行驶了$\frac{105}{4}$千米，自行车从出发到再次相遇行驶了$\frac{57}{4}$千米.