2025年教材帮七年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年教材帮七年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1(知识点1)若$(k + 2)x^{|k| - 1} + 5 < 0$是关于$x$的一元一次不等式,则$k$的值为 ( )
A. 2
B. 1
C. ±2
D. ±1
A. 2
B. 1
C. ±2
D. ±1
答案:
A 因为$(k + 2)x^{|k| - 1}+5 < 0$是关于$x$的一元一次不等式,所以$\begin{cases}|k| - 1 = 1\\k + 2\neq0\end{cases}$,解得$k = 2$.
易错点拨:忽略未知数的系数不为0致错
本题的易错点是直接令$|k| - 1 = 1$进行求解,忽略了$k + 2\neq0$这一限制条件.
易错点拨:忽略未知数的系数不为0致错
本题的易错点是直接令$|k| - 1 = 1$进行求解,忽略了$k + 2\neq0$这一限制条件.
2(知识点2)下列说法中,错误的是 ( )
A. 不等式$x < 5$的整数解有无数个
B. 不等式$x > - 5$的负整数解有有限个
C. $x < - 4$是不等式$- 2x < 8$的解集
D. - 40是不等式$2x < - 8$的一个解
A. 不等式$x < 5$的整数解有无数个
B. 不等式$x > - 5$的负整数解有有限个
C. $x < - 4$是不等式$- 2x < 8$的解集
D. - 40是不等式$2x < - 8$的一个解
答案:
C 不等式$x < 5$的整数解为小于5的所有整数,有无数个,故选项A不符合题意;不等式$x > - 5$的负整数解有$-4$,$-3$,$-2$,$-1$,故选项B不符合题意;取一个大于$-4$的数代入不等式$-2x < 8$,如$x = 0$,不等式成立,所以$x < - 4$不是不等式$-2x < 8$的解集,故选项C符合题意;将$x = - 40$代入,得$2\times(-40)= - 80 < - 8$成立,故选项D不符合题意.
3(知识点2)如图所示的不等式的解集是 ( )
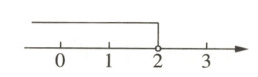
A. $x > 2$
B. $x < 2$
C. $x\geq2$
D. $x\leq2$

A. $x > 2$
B. $x < 2$
C. $x\geq2$
D. $x\leq2$
答案:
B
4(知识点2)(连云港期末)若$x = - 1$是不等式$2x + m\leq0$的解,则$m$的值不可能是 ( )
A. 0
B. 1
C. 2
D. 3
A. 0
B. 1
C. 2
D. 3
答案:
D 因为$x = - 1$是不等式$2x + m\leqslant0$的解,所以$-2 + m\leqslant0$,所以$m\leqslant2$.
5(知识点2)不等式$x\leq4$的非负整数解是_______.
答案:
0,1,2,3,4
6(知识点2)已知关于$x$的不等式$x\geq a - 1$的解集如图所示,则$a$的值为______.
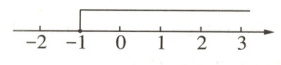
答案:
0 因为数轴上表示的不等式的解集为$x\geqslant - 1$,所以$a - 1 = - 1$,解得$a = 0$.
7(知识点2)在数轴上表示下列不等式的解集.
(1)$x\geq - 1$; (2)$x < - 2$;
(3)$x > 2\frac{1}{2}$; (4)$x\leq - 1.5$.
(1)$x\geq - 1$; (2)$x < - 2$;
(3)$x > 2\frac{1}{2}$; (4)$x\leq - 1.5$.
答案:
解:
(1)如图所示.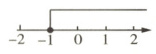
(2)如图所示.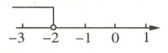
(3)如图所示.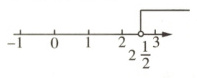
(4)如图所示.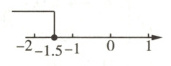
解:
(1)如图所示.

(2)如图所示.
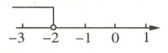
(3)如图所示.

(4)如图所示.

8(2024·宿迁宿城区期末)如图表示某个关于$x$的不等式的解集,若$x = m - 2$是该不等式的一个解,则$m$的取值范围是_______.


答案:
$m < - 5$ 由题图可知,关于$x$的不等式的解集为$x > 3m + 8$.
因为$x = m - 2$是该不等式的一个解,
所以$m - 2 > 3m + 8$,
所以$m < - 5$.
因为$x = m - 2$是该不等式的一个解,
所以$m - 2 > 3m + 8$,
所以$m < - 5$.
9 新课标 开放性试题 试写出一个不等式,使它的解集分别满足下列条件:
(1)不等式的正整数解只有1,2,3;
(2)不等式的非正整数解只有 - 2, - 1,0.
(1)不等式的正整数解只有1,2,3;
(2)不等式的非正整数解只有 - 2, - 1,0.
答案:
解:
(1)答案不唯一,如$x < 4$.
(2)答案不唯一,如$x > - 3$.
(1)答案不唯一,如$x < 4$.
(2)答案不唯一,如$x > - 3$.
10 求不等式$x - 3 < 0$,$x - 3 > 0$的解集,我们可以从相应的方程$x - 3 = 0$入手,方程$x - 3 = 0$的解是$x = 3$,大于3的所有的数都能使$x - 3 > 0$成立,小于3的所有的数都能使$x - 3 < 0$成立,所以$x - 3 < 0$的解集是$x < 3$,$x - 3 > 0$的解集是$x > 3$. 利用数轴能直观地反映它们之间的关系,方程的解可以用数轴上的点$A$表示(如图1),点$A$将数轴上的其余点分成两部分:点$A$左边的点(如图2)表示的数是$x < 3$,它是不等式$x - 3 < 0$的解集;点$A$右边的点(如图3)表示的数是$x > 3$,它是不等式$x - 3 > 0$的解集. 尝试用不等式与方程的这种关系,求出不等式$2x + 1 < 5$的解集.


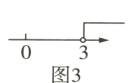



答案:
解:从相应的方程$2x + 1 = 5$入手,方程$2x + 1 = 5$的解是$x = 2$,大于2的所有的数都能使$2x + 1 > 5$成立,小于2的所有的数都能使$2x + 1 < 5$成立,所以$2x + 1 < 5$的解集是$x < 2$. 利用数轴能直观地反映它们之间的关系,方程的解可以用数轴上的点$M$表示(如图1),点$M$左边的点(如图2)表示的数是$x < 2$,它是不等式$2x + 1 < 5$的解集.

解:从相应的方程$2x + 1 = 5$入手,方程$2x + 1 = 5$的解是$x = 2$,大于2的所有的数都能使$2x + 1 > 5$成立,小于2的所有的数都能使$2x + 1 < 5$成立,所以$2x + 1 < 5$的解集是$x < 2$. 利用数轴能直观地反映它们之间的关系,方程的解可以用数轴上的点$M$表示(如图1),点$M$左边的点(如图2)表示的数是$x < 2$,它是不等式$2x + 1 < 5$的解集.

查看更多完整答案,请扫码查看


