2025年教材帮七年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年教材帮七年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7 一艘轮船在相距90千米的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6小时,从乙地到甲地逆流航行比从甲地到乙地顺流航行多用4小时.
(1)求该轮船在静水中的速度和水流速度.
(2)若在甲、乙两地之间建立丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,问甲、丙两地相距多少千米.
(1)求该轮船在静水中的速度和水流速度.
(2)若在甲、乙两地之间建立丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,问甲、丙两地相距多少千米.
答案:
解:
(1)设该轮船在静水中的速度是x千米/时,水流速度是y千米/时.
依题意,得$\begin{cases}6(x + y) = 90,\\(6 + 4)(x - y) = 90,\end{cases}$解得$\begin{cases}x = 12,\\y = 3.\end{cases}$
答:该轮船在静水中的速度是12千米/时,水流速度是3千米/时.
(2)设甲、丙两地相距a千米,则乙、丙两地相距$(90 - a)$千米.
依题意,得$\frac{a}{12 + 3} = \frac{90 - a}{12 - 3}$,解得$a = \frac{225}{4}$.
答:甲、丙两地相距$\frac{225}{4}$千米.
(1)设该轮船在静水中的速度是x千米/时,水流速度是y千米/时.
依题意,得$\begin{cases}6(x + y) = 90,\\(6 + 4)(x - y) = 90,\end{cases}$解得$\begin{cases}x = 12,\\y = 3.\end{cases}$
答:该轮船在静水中的速度是12千米/时,水流速度是3千米/时.
(2)设甲、丙两地相距a千米,则乙、丙两地相距$(90 - a)$千米.
依题意,得$\frac{a}{12 + 3} = \frac{90 - a}{12 - 3}$,解得$a = \frac{225}{4}$.
答:甲、丙两地相距$\frac{225}{4}$千米.
8 随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需5 200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒. 问打折后购买这批粽子比不打折节省了多少钱?
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒. 问打折后购买这批粽子比不打折节省了多少钱?
答案:
解:
(1)设打折前甲品牌粽子每盒x元,乙品牌粽子每盒y元.
根据题意,得$\begin{cases}6x + 3y = 660,\\50×0.8x + 40×0.75y = 5200,\end{cases}$
解得$\begin{cases}x = 70,\\y = 80.\end{cases}$
答:打折前甲品牌粽子每盒70元,乙品牌粽子每盒80元.
(2)$80×70×(1 - 0.8) + 100×80×(1 - 0.75) = 3120$(元).
答:打折后购买这批粽子比不打折节省了3120元.
(1)设打折前甲品牌粽子每盒x元,乙品牌粽子每盒y元.
根据题意,得$\begin{cases}6x + 3y = 660,\\50×0.8x + 40×0.75y = 5200,\end{cases}$
解得$\begin{cases}x = 70,\\y = 80.\end{cases}$
答:打折前甲品牌粽子每盒70元,乙品牌粽子每盒80元.
(2)$80×70×(1 - 0.8) + 100×80×(1 - 0.75) = 3120$(元).
答:打折后购买这批粽子比不打折节省了3120元.
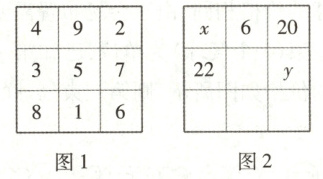
9 (武汉中考)幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格. 将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图1就是一个幻方. 图2是一个未完成的幻方,则x与y的和是( )
A.9
B.10
C.11
D.12

A.9
B.10
C.11
D.12
答案:
D 因为每一横行、每一竖列以及两条对角线上的3个数之和相等,
所以左下角的数为$6 + 20 + x - x - 22 = 4$,
所以中间的数为$x + 6 + 20 - 20 - 4 = x + 2$,或$x + 6 + 20 - 22 - y = x - y + 4$,
右下角的数为$6 + 20 + x - x - (x + 2) = 24 - x$,或$x + 6 + 20 - 20 - y = x - y + 6$,
所以$\begin{cases}x + 2 = x - y + 4,\\24 - x = x - y + 6,\end{cases}$解得$\begin{cases}x = 10,\\y = 2,\end{cases}$
所以$x + y = 12$.
所以左下角的数为$6 + 20 + x - x - 22 = 4$,
所以中间的数为$x + 6 + 20 - 20 - 4 = x + 2$,或$x + 6 + 20 - 22 - y = x - y + 4$,
右下角的数为$6 + 20 + x - x - (x + 2) = 24 - x$,或$x + 6 + 20 - 20 - y = x - y + 6$,
所以$\begin{cases}x + 2 = x - y + 4,\\24 - x = x - y + 6,\end{cases}$解得$\begin{cases}x = 10,\\y = 2,\end{cases}$
所以$x + y = 12$.
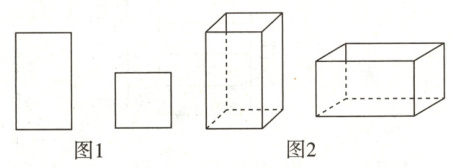
10 用图1中的长方形和正方形纸板作为侧面和底面,做成如图2所示的竖式和横式的两种无盖纸盒. 现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则m + n的值可能是( )
A.2 022
B.2 023
C.2 024
D.2 025

A.2 022
B.2 023
C.2 024
D.2 025
答案:
D 设可以做竖式纸盒x个,横式纸盒y个.
由题意可得,$\begin{cases}4x + 3y = n,\\x + 2y = m.\end{cases}$
则$m + n = 5x + 5y = 5(x + y)$.
由于x,y均为整数,故$m + n$为5的倍数,选项中2025是5的倍数. 故选D.
由题意可得,$\begin{cases}4x + 3y = n,\\x + 2y = m.\end{cases}$
则$m + n = 5x + 5y = 5(x + y)$.
由于x,y均为整数,故$m + n$为5的倍数,选项中2025是5的倍数. 故选D.
11 (扬州中考)古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由A,B两工程队先后接力完成. A工程队每天整治12米,B工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:$\begin{cases}x + y = \\12x + 8y =\end{cases}$ 乙:$\begin{cases}x + y = \\\frac{x}{12} + \frac{y}{8} =\end{cases}$
根据甲、乙两名同学所列的方程组,请你分别指出未知数x,y表示的意义,然后补全甲、乙两名同学所列的方程组.
(2)求A,B两工程队分别整治河道多少米.(写出完整的解答过程)
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:$\begin{cases}x + y = \\12x + 8y =\end{cases}$ 乙:$\begin{cases}x + y = \\\frac{x}{12} + \frac{y}{8} =\end{cases}$
根据甲、乙两名同学所列的方程组,请你分别指出未知数x,y表示的意义,然后补全甲、乙两名同学所列的方程组.
(2)求A,B两工程队分别整治河道多少米.(写出完整的解答过程)
答案:
解:
(1)甲:x表示A工程队工作的天数,y表示B工程队工作的天数. 乙:x表示A工程队整治河道的长度,y表示B工程队整治河道的长度.
补全甲、乙两名同学所列的方程组如下.
甲:$\begin{cases}x + y = 20,\\12x + 8y = 180.\end{cases}$ 乙:$\begin{cases}x + y = 180,\\\frac{x}{12} + \frac{y}{8} = 20.\end{cases}$
(2)由
(1)中乙同学所列的方程组可解得$\begin{cases}x = 60,\\y = 120.\end{cases}$
所以A,B两工程队分别整治河道60米、120米.
(1)甲:x表示A工程队工作的天数,y表示B工程队工作的天数. 乙:x表示A工程队整治河道的长度,y表示B工程队整治河道的长度.
补全甲、乙两名同学所列的方程组如下.
甲:$\begin{cases}x + y = 20,\\12x + 8y = 180.\end{cases}$ 乙:$\begin{cases}x + y = 180,\\\frac{x}{12} + \frac{y}{8} = 20.\end{cases}$
(2)由
(1)中乙同学所列的方程组可解得$\begin{cases}x = 60,\\y = 120.\end{cases}$
所以A,B两工程队分别整治河道60米、120米.
查看更多完整答案,请扫码查看


