搜索
2025年教材帮七年级数学下册苏科版
注：目前有些书本章节名称可能整理的还不是很完善，但都是按照顺序排列的，请同学们按照顺序仔细查找。练习册 2025年教材帮七年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的，请勿直接抄袭。
1（盐城期中）下列计算正确的是（ ）
A. $3x^{3}\cdot2x^{2}y = 6x^{5}$
B. $3a^{2}\cdot2a^{3}=6a^{5}$
C. $(-2x)\cdot(-5x^{2}y)= - 10x^{3}y$
D. $(-2xy)\cdot(-3x^{2}y)=6x^{3}y$
A. $3x^{3}\cdot2x^{2}y = 6x^{5}$
B. $3a^{2}\cdot2a^{3}=6a^{5}$
C. $(-2x)\cdot(-5x^{2}y)= - 10x^{3}y$
D. $(-2xy)\cdot(-3x^{2}y)=6x^{3}y$
答案：
B $3x^{3}\cdot2x^{2}y = 6x^{5}y$，故 A 错误；$3a^{2}\cdot2a^{3}=6a^{5}$，故 B 正确；$( - 2x)\cdot( - 5x^{2}y)=10x^{3}y$，故 C 错误；$( - 2xy)\cdot( - 3x^{2}y)=6x^{3}y^{2}$，故 D 错误.
2（2024·扬州邗江区模拟）若( )$\cdot3a^{2}b = 9a^{3}b$，则括号内应填的单项式是（ ）
A. $a$
B. $3a$
C. $3b$
D. $3ab$
A. $a$
B. $3a$
C. $3b$
D. $3ab$
答案：
B
3 若$(a^{m}b^{2})\cdot(ab^{n}) = a^{5}b^{3}$，则$m + n$的值为（ ）
A. 3
B. 4
C. 5
D. 6
A. 3
B. 4
C. 5
D. 6
答案：
C 因为$(a^{m}b^{2})\cdot(ab^{n})=a^{m + 1}b^{n + 2}=a^{5}b^{3}$，所以$m + 1 = 5$，$n + 2 = 3$，所以$m = 4$，$n = 1$，所以$m + n = 5$.
4 计算$(2m^{2}n^{-3})^{-3}\cdot(-mn^{-2})^{-2}$，把结果化为只含有正整数指数幂的形式为______。
答案：
$\frac{n^{13}}{8m^{8}}$ $(2m^{2}n^{-3})^{-3}\cdot( - mn^{-2})^{-2}=(2^{-3}m^{-6}n^{9})\cdot(m^{-2}n^{4})=2^{-3}m^{-8}n^{13}=\frac{n^{13}}{8m^{8}}$.
5 一个长方体的长为$8\times10^{5}$cm，宽为$5\times10^{6}$cm，高为$9\times10^{8}$cm，则这个长方体的体积为______$cm^{3}$。
答案：
$3.6\times10^{21}$ 由题意，得$(8\times10^{5})\times(5\times10^{6})\times(9\times10^{8}) = 360\times10^{19}=3.6\times10^{21}(cm^{3})$，所以这个长方体的体积为$3.6\times10^{21}cm^{3}$.
6（易错题）计算：
(1)$(-5ab^{2}x)\cdot(-\frac{3}{10}a^{2}bx^{3}y)$；
(2)$2xy^{2}\cdot(-3x^{2}y^{3})^{2}$；
(3)$2x^{2}\cdot x^{6}+(-x^{2})^{3}\cdot(-x)^{2}$；
(4)$(-2xy^{2})^{2}-3xy^{3}\cdot(-2xy)$。
(1)$(-5ab^{2}x)\cdot(-\frac{3}{10}a^{2}bx^{3}y)$；
(2)$2xy^{2}\cdot(-3x^{2}y^{3})^{2}$；
(3)$2x^{2}\cdot x^{6}+(-x^{2})^{3}\cdot(-x)^{2}$；
(4)$(-2xy^{2})^{2}-3xy^{3}\cdot(-2xy)$。
答案：
解：
(1)原式$=[( - 5)\times( - \frac{3}{10})]\cdot(a\cdot a^{2})\cdot(b^{2}\cdot b)\cdot(x\cdot x^{3})\cdot y=\frac{3}{2}a^{3}b^{3}x^{4}y$.
(2)原式$=2xy^{2}\cdot9x^{4}y^{6}=18x^{5}y^{8}$.
(3)原式$=2x^{8}+( - x^{6})\cdot x^{2}=2x^{8}-x^{8}=x^{8}$.
(4)原式$=( - 2)^{2}\cdot(xy^{2})^{2}-3xy^{3}\cdot( - 2xy)=4x^{2}y^{4}+3xy^{3}\cdot2xy = 4x^{2}y^{4}+6x^{2}y^{4}=10x^{2}y^{4}$.
易错点拨：此题容易出现的错误是弄错系数的符号或结果中漏掉只在一个单项式中出现的字母.
(1)原式$=[( - 5)\times( - \frac{3}{10})]\cdot(a\cdot a^{2})\cdot(b^{2}\cdot b)\cdot(x\cdot x^{3})\cdot y=\frac{3}{2}a^{3}b^{3}x^{4}y$.
(2)原式$=2xy^{2}\cdot9x^{4}y^{6}=18x^{5}y^{8}$.
(3)原式$=2x^{8}+( - x^{6})\cdot x^{2}=2x^{8}-x^{8}=x^{8}$.
(4)原式$=( - 2)^{2}\cdot(xy^{2})^{2}-3xy^{3}\cdot( - 2xy)=4x^{2}y^{4}+3xy^{3}\cdot2xy = 4x^{2}y^{4}+6x^{2}y^{4}=10x^{2}y^{4}$.
易错点拨：此题容易出现的错误是弄错系数的符号或结果中漏掉只在一个单项式中出现的字母.
7（苏州姑苏区期中）已知$-2x^{m}y^{2}$与$4x^{2}y^{n - 1}$的积与$-x^{4}y^{3}$是同类项，则$mn =$（ ）
A. 2
B. 3
C. 4
D. 5
A. 2
B. 3
C. 4
D. 5
答案：
C 因为$-2x^{m}y^{2}$与$4x^{2}y^{n - 1}$的积与$-x^{4}y^{3}$是同类项，$( - 2x^{m}y^{2})\cdot(4x^{2}y^{n - 1})=-8x^{m + 2}y^{n + 1}$，所以$m + 2 = 4$，$n + 1 = 3$，解得$m = 2$，$n = 2$，所以$mn = 4$.
8 先化简，再求值：$a^{3}\cdot(-b^{3})+(-\frac{1}{2}ab^{2})^{3}$，其中$a = \frac{1}{4}$，$b = 4$。
答案：
解：因为$a^{3}\cdot( - b^{3})+( - \frac{1}{2}ab^{2})^{3}=-a^{3}b^{3}-\frac{1}{8}a^{3}b^{6}$，所以当$a=\frac{1}{4}$，$b = 4$时，原式$=-( \frac{1}{4})^{3}\times4^{3}-\frac{1}{8}\times( \frac{1}{4})^{3}\times4^{6}=-1-\frac{1}{8}\times64=-9$.
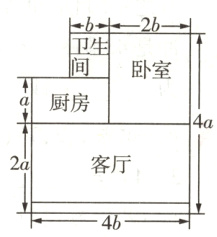
9 如图是小李家住房的平面示意图，小李打算在卧室和客厅里铺上木地板.请你帮他算一算，他需要买的木地板的面积至少是多少.
答案：
解：由题图知，卧室和客厅的面积为$2a\cdot4b+(4a - 2a)\cdot2b = 12ab$，所以他需要买的木地板的面积至少是$12ab$.
10（创新题）定义：
=3abc，
=$-4x^{z}w^{y}$，求
。
=3abc，=$-4x^{z}w^{y}$，求。
答案：
解：
$=9mn\cdot( - 4n^{2}m^{5})=-36m^{6}n^{3}$.
解：
$=9mn\cdot( - 4n^{2}m^{5})=-36m^{6}n^{3}$. 查看更多完整答案，请扫码查看
