2025年教材帮七年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年教材帮七年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1 下列运算中不正确的是( )
A. $3xy-(x^{2}-2xy)=5xy - x^{2}$
B. $5x(2x^{2}-y)=10x^{3}-5xy$
C. $5mn(2m + 3n - 1)=10m^{2}n+15mn^{2}-1$
D. $(ab)^{2}(2ab^{2}-c)=2a^{3}b^{4}-a^{2}b^{2}c$
A. $3xy-(x^{2}-2xy)=5xy - x^{2}$
B. $5x(2x^{2}-y)=10x^{3}-5xy$
C. $5mn(2m + 3n - 1)=10m^{2}n+15mn^{2}-1$
D. $(ab)^{2}(2ab^{2}-c)=2a^{3}b^{4}-a^{2}b^{2}c$
答案:
1.C 选项A中,因为$3xy-(x^{2}-2xy)=3xy - x^{2}+2xy = 5xy - x^{2}$,所以选项A正确;选项B中,因为$5x(2x^{2}-y)=10x^{3}-5xy$,所以选项B正确;选项C中,因为$5mn(2m + 3n - 1)=10m^{2}n + 15mn^{2}-5mn$,所以选项C不正确;选项D中,因为$(ab)^{2}(2ab^{2}-c)=a^{2}b^{2}(2ab^{2}-c)=2a^{3}b^{4}-a^{2}b^{2}c$,所以选项D正确.故选C.
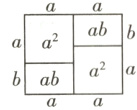
2 (2024·宿迁期中)通过计算几何图形的面积可表示一些代数恒等式,如图可表示的代数恒等式是( )
A. $(a - b)^{2}=a^{2}-2ab + b^{2}$
B. $(a + b)^{2}=a^{2}+2ab + b^{2}$
C. $2a(a + b)=2a^{2}+2ab$
D. $(a + b)(a - b)=a^{2}-b^{2}$

A. $(a - b)^{2}=a^{2}-2ab + b^{2}$
B. $(a + b)^{2}=a^{2}+2ab + b^{2}$
C. $2a(a + b)=2a^{2}+2ab$
D. $(a + b)(a - b)=a^{2}-b^{2}$
答案:
2.C 大长方形的面积为$2a(a + b)$,四个小图形的面积之和为$a^{2}+a^{2}+ab + ab = 2a^{2}+2ab$,两者相等,即$2a(a + b)=2a^{2}+2ab$.
3 (泰州期中)要使$-x^{3}(x^{2}+ax + 1)+2x^{4}$的化简结果中不含有$x$的四次项,则$a$等于( )
A. 1
B. 2
C. 3
D. 4
A. 1
B. 2
C. 3
D. 4
答案:
3.B 原式$=-x^{5}-ax^{4}-x^{3}+2x^{4}=-x^{5}+(2 - a)\cdot x^{4}-x^{3}$.因为$-x^{3}(x^{2}+ax + 1)+2x^{4}$的化简结果中不含有$x$的四次项,所以$2 - a = 0$,解得$a = 2$,故选B.
4 (1)(2024·徐州铜山区期中)计算:$-3m(m^{2}-6m + 1)=$_______.
答案:
$-3m^{3}+18m^{2}-3m$
(2)(苏州高新区期中)计算:$(3x^{2}y - 2x + 1)\cdot(-2xy)=$______.
答案:
$-6x^{3}y^{2}+4x^{2}y - 2xy$
5 (易错题)若$2x(x - 1)-x(2x - 5)=12$,则$x=$______.
答案:
4 因为$2x(x - 1)-x(2x - 5)=12$,所以$2x^{2}-2x-2x^{2}+5x = 12$,即$3x = 12$,所以$x = 4$.
6 计算:(1)$x^{2}y(2xy - 5)-2xy\cdot(x^{2}y - x)$;
(2)$6mn^{2}\cdot(2-\frac{1}{3}mn^{4})+(\frac{1}{2}mn^{3})^{2}$;
(3)$3a^{2}(a^{3}b^{2}-2a)-4a\cdot(-a^{2}b)^{2}$;
(4)$3a(2a^{2}-4a + 3)-2a^{2}(3a + 4)$.
(2)$6mn^{2}\cdot(2-\frac{1}{3}mn^{4})+(\frac{1}{2}mn^{3})^{2}$;
(3)$3a^{2}(a^{3}b^{2}-2a)-4a\cdot(-a^{2}b)^{2}$;
(4)$3a(2a^{2}-4a + 3)-2a^{2}(3a + 4)$.
答案:
解:
(1)原式$=2x^{3}y^{2}-5x^{2}y - 2x^{3}y^{2}+2x^{2}y=-3x^{2}y$.
(2)原式$=12mn^{2}-2m^{2}n^{6}+\frac{1}{4}m^{2}n^{6}=12mn^{2}-\frac{7}{4}m^{2}n^{6}$.
(3)原式$=3a^{5}b^{2}-6a^{3}-4a\cdot a^{4}b^{2}=3a^{5}b^{2}-6a^{3}-4a^{5}b^{2}=-a^{5}b^{2}-6a^{3}$.
(4)原式$=6a^{3}-12a^{2}+9a - 6a^{3}-8a^{2}=-20a^{2}+9a$.
(1)原式$=2x^{3}y^{2}-5x^{2}y - 2x^{3}y^{2}+2x^{2}y=-3x^{2}y$.
(2)原式$=12mn^{2}-2m^{2}n^{6}+\frac{1}{4}m^{2}n^{6}=12mn^{2}-\frac{7}{4}m^{2}n^{6}$.
(3)原式$=3a^{5}b^{2}-6a^{3}-4a\cdot a^{4}b^{2}=3a^{5}b^{2}-6a^{3}-4a^{5}b^{2}=-a^{5}b^{2}-6a^{3}$.
(4)原式$=6a^{3}-12a^{2}+9a - 6a^{3}-8a^{2}=-20a^{2}+9a$.
7 (2024·无锡梁溪区期中)若$5^{m}=6$,$6^{n}=5$,则$2m(3m - n)-m(2n + 6m)+3$的值为_______.
答案:
-1 $\because 5^{m}=6,6^{n}=5$,
$\therefore (6^{n})^{m}=5^{m}=6$,即$6^{mn}=6$,
$\therefore mn = 1$.
原式$=2m(3m - n)-m(2n + 6m)+3$
$=6m^{2}-2mn - 2mn - 6m^{2}+3$
$=3 - 4mn$
$=3 - 4$
$=-1$.
$\therefore (6^{n})^{m}=5^{m}=6$,即$6^{mn}=6$,
$\therefore mn = 1$.
原式$=2m(3m - n)-m(2n + 6m)+3$
$=6m^{2}-2mn - 2mn - 6m^{2}+3$
$=3 - 4mn$
$=3 - 4$
$=-1$.
8 先化简,再求值:$3x(x - 2y)-[3x^{2}-2y + 2(xy + y)]$,其中$x=-\frac{1}{2}$,$y=-3$.
答案:
解:原式$=3x^{2}-6xy-(3x^{2}-2y + 2xy + 2y)=3x^{2}-6xy - 3x^{2}+2y - 2xy - 2y=-8xy$,
当$x = -\frac{1}{2},y = -3$时,
原式$=-8\times(-\frac{1}{2})\times(-3)=-12$.
当$x = -\frac{1}{2},y = -3$时,
原式$=-8\times(-\frac{1}{2})\times(-3)=-12$.
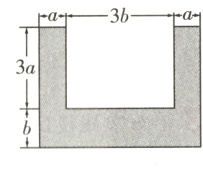
9 如图,阴影部分是某零件横截面的示意图,请计算图中阴影部分的面积.

答案:
解:把图形进行分割,阴影部分的面积可看成三个长方形的面积之和,则阴影部分的面积为$b\cdot(3b + 2a)+2\cdot a\cdot 3a = 3b^{2}+2ab + 6a^{2}$.
10 某同学在计算一个多项式乘$-3x^{2}$时,因抄错运算符号,算成了加上$-3x^{2}$,得到的结果是$x^{2}-4x + 1$,那么正确的计算结果是多少?
答案:
解:这个多项式是$x^{2}-4x + 1-(-3x^{2})=4x^{2}-4x + 1$,正确的计算结果是$(4x^{2}-4x + 1)\cdot(-3x^{2})=-12x^{4}+12x^{3}-3x^{2}$.
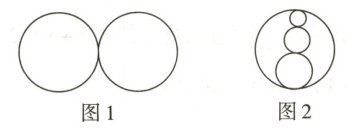
11 某公园计划建一个形状如图1所示的喷水池.
(1)有人建议改为如图2所示的形状,外观直径不变,三个小圆的圆心与大圆的圆心共线,只是担心原来备好的材料不够,请你比较这两种方案,确定哪一种需要的材料多(即比较哪个周长更长).
(2)若将三个小圆改成$n$个小圆,所有圆的圆心均共线,则原来备好的材料是否够用?请说明理由.
(1)有人建议改为如图2所示的形状,外观直径不变,三个小圆的圆心与大圆的圆心共线,只是担心原来备好的材料不够,请你比较这两种方案,确定哪一种需要的材料多(即比较哪个周长更长).
(2)若将三个小圆改成$n$个小圆,所有圆的圆心均共线,则原来备好的材料是否够用?请说明理由.

答案:
解:
(1)设题图中每个大圆的直径为$d$,周长为$l$,题图2中的三个小圆的直径分别是$d_{1},d_{2},d_{3}$,周长分别是$l_{1},l_{2},l_{3}$,则$d = d_{1}+d_{2}+d_{3}$.
由题意知,$l=\pi d=\pi(d_{1}+d_{2}+d_{3})=\pi d_{1}+\pi d_{2}+\pi d_{3}=l_{1}+l_{2}+l_{3}$,
则题图中每个大圆的周长与题图2中三个小圆周长的和相等,即这两种方案需要的材料一样多.
(2)够用.理由如下:
设大圆直径为$d$,周长为$l$,$n$个小圆的直径分别是$d_{1},d_{2},\cdots,d_{n}$,周长分别是$l_{1},l_{2},\cdots,l_{n}$,
则$l=\pi d=\pi(d_{1}+d_{2}+\cdots + d_{n})=\pi d_{1}+\pi d_{2}+\cdots+\pi d_{n}=l_{1}+l_{2}+\cdots + l_{n}$,
所以一个大圆的周长与$n$个小圆周长的和相等,即原来备好的材料够用.
(1)设题图中每个大圆的直径为$d$,周长为$l$,题图2中的三个小圆的直径分别是$d_{1},d_{2},d_{3}$,周长分别是$l_{1},l_{2},l_{3}$,则$d = d_{1}+d_{2}+d_{3}$.
由题意知,$l=\pi d=\pi(d_{1}+d_{2}+d_{3})=\pi d_{1}+\pi d_{2}+\pi d_{3}=l_{1}+l_{2}+l_{3}$,
则题图中每个大圆的周长与题图2中三个小圆周长的和相等,即这两种方案需要的材料一样多.
(2)够用.理由如下:
设大圆直径为$d$,周长为$l$,$n$个小圆的直径分别是$d_{1},d_{2},\cdots,d_{n}$,周长分别是$l_{1},l_{2},\cdots,l_{n}$,
则$l=\pi d=\pi(d_{1}+d_{2}+\cdots + d_{n})=\pi d_{1}+\pi d_{2}+\cdots+\pi d_{n}=l_{1}+l_{2}+\cdots + l_{n}$,
所以一个大圆的周长与$n$个小圆周长的和相等,即原来备好的材料够用.
查看更多完整答案,请扫码查看


