《2025年小升初考点汇编数学》

7. 吸烟不仅有害健康而且浪费钱，如果一位吸烟者每天吸一包11元的香烟，那么他每年花在吸烟上的钱大约是(　　　)元。
A. 30000
B. 4000
C. 5000
D. 7000

答案： 7.B

8. 小乐喝了一杯牛奶的$\frac{1}{6}$，然后加满水，又喝了一杯的$\frac{1}{3}$，再倒满水，又喝了$\frac{1}{2}$杯后，继续加满水，最后把一杯喝完了。小乐喝了(　　　)杯牛奶和(　　　)杯水。
A. 1
B. $\frac{1}{2}$
C. $\frac{5}{6}$
D. $\frac{2}{3}$

答案： 8.A

三、口算。
$\frac{6}{7}$×$\frac{1}{6}$ = 　　　　2.5×$\frac{3}{5}$ = 　　　$\frac{1}{4}$ + $\frac{1}{2}$ = 　
$\frac{3}{4}$ - $\frac{2}{3}$ = 　　　0.125×8 = 　　0.4×0.25 = 　
36÷$\frac{4}{9}$ = 　　　9.7 + 0.03 = 　　4.2÷1% = 　
$\frac{4}{7}$×2.1 = 　　496 + 301≈ 　　502 - 399≈ 　　798×9≈ 　　　643÷79≈ 　　　3.99×7.01≈

答案： $\frac{1}{7}$ 1.5 $\frac{3}{4}$ $\frac{1}{12}$ 1 0.1 81 9.73 420 1.2 800 100 7200 8 28

四、用竖式计算。
5 - 2.09 = 　　　　　　　　428×57 = 　
43.25 + 2.57 = 　　　　　0.036×1.5 = 　
104.7÷6.25 = 　　　　　87÷0.06 = 　
6.05×15.8 = 　　　　　　0.161÷2.3 = 　

答案： 2.91 24396 45.82 0.054 16.752 1450 95.59 0.07

冲刺名校
五、甲数除以乙数的商是1.5，若甲数增加15，则甲数是乙数的4倍。原来甲数是多少?

答案： $15\div(4 - 1.5)\times1.5 = 9$

考点1 四则混合运算
例1 计算:(1)$\frac{9}{4}×\frac{8}{5}÷1.7$
(2)$0.5×[5\frac{1}{5}÷(3 - 2.5×\frac{7}{8})]$

答案： 【点拨】此题综合考查四则混合运算的顺序。
(1)按照从左到右的顺序计算;
(2)题中含有括号,要先算小括号里的,再算中括号里的,最后算括号外面的。
【解答】
(1)原式$=\frac{9}{4}×\frac{8}{5}×\frac{10}{17}$
$=\frac{36}{17}$
(2)原式$=0.5×[\frac{26}{5}÷(3 - \frac{5}{2}×\frac{7}{8})]$
$=0.5×[\frac{26}{5}÷(3 - \frac{35}{16})]$
$=0.5×[\frac{26}{5}÷\frac{13}{16}]$
$=0.5×\frac{26}{5}×\frac{16}{13}=\frac{16}{5}$

考点2 简便运算
例2 简算。
(1)$478 - 256 - 144$
(2)$125×32×25$
(3)$4.38×5.6 + 56.2×0.56$

答案： 【点拨】此题考查运算定律和性质在简便运算中的应用。
(1)题中的256和144合起来是400,所以可以根据减法的性质先计算256 + 144,最后结果为78。
(2)题根据125×8 = 1000和25×4 = 100的特殊性,可以先将32拆成8×4,再利用乘法结合律计算(125×8)×(4×25),最后结果为100000。
(3)题根据5.6和0.56的关系,可以先把56.2×0.56化成5.62×5.6,再利用乘法分配律计算。
【解答】
(1) 478 - 256 - 144
$=478 - (256 + 144)$
$=478 - 400$
$=78$
(2) 125×32×25
$=(125×8)×(4×25)$
$=1000×100$
$=100000$
(3) 4.38×5.6 + 56.2×0.56
$=4.38×5.6 + 5.62×5.6$
$=5.6×(4.38 + 5.62)$
$=56$

考点3 找规律简便运算
例3 计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}$。

答案：
【点拨】这一题可以分步通分,分步求出和,也可以一次性通分再求和。但这里面隐藏了一个规律。$\frac{1}{2}$、$\frac{1}{4}$、$\frac{1}{8}$和$\frac{1}{16}$都是依次减少一半。不妨借助于一个正方形(如右图)来看,它们加起来的和等于整数“1”减去$\frac{1}{16}$。所以本题的结果可以用$1-\frac{1}{16}$来计算。

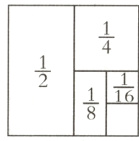
【解答】$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=1-\frac{1}{16}=\frac{15}{16}$
【点评】对于比较复杂的算式,在计算时不能去“硬”算,而是要通过寻找规律找到简便的算法。在遇到较大的数或较复杂的计算时,要多去想想,有没有规律,可不可以简便计算,平时解题的过程中要注意多积累。