《2025年名校课堂内外九年级数学下册人教版》

3.(随州市中考)如图1,平面直角坐标系xOy中,抛物线y=ax²+bx + c过点A(−1,0),B(2,0)和C(0,2),连接BC,点P(m,n)(m ＞0)为抛物线上一动点，过点P作PN⊥x轴交直线BC于点M,交x轴于点N.
　 　　　
　(2)如图2,连接OM,当△OCM为等腰三角形时,求m的值;
　(3)当P点在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应),若存在,直接写出点P和点Q的坐标;若不存在,请说明理由.

答案：
(1) 解：抛物线的解析式为：y = -x² + x + 2。直线BC的解析式为：y = -x + 2。
(2) 因为点M在直线BC上，且P(m, n)，所以点M的坐标为(m, -m + 2)。所以OC = 2，CM² = (m - 0)² + (-m + 2 - 2)² = 2m²，OM² = m² + (-m + 2)² = 2m² - 4m + 4。当△OCM为等腰三角形时：① 若CM = OM，则CM² = OM²，即2m² = 2m² - 4m + 4，解得m = 1。② 若CM = OC，则CM² = OC²，即2m² = 4，解得m = $\sqrt{2}$或m = -$\sqrt{2}$(舍去)。③ 若OM = OC，则OM² = OC²，即2m² - 4m + 4 = 4，解得m = 0(舍去)或m = 2。综上，m = 1或m = $\sqrt{2}$或m = 2。
(3) P($\sqrt{2}$,$\sqrt{2}$)，Q(0,$\sqrt{2}$ - 1)或P(1 + $\sqrt{3}$,-1 - $\sqrt{3}$)，Q(0, 1)或P($\frac{1 + \sqrt{13}}{3}$,$\frac{7 + \sqrt{13}}{9}$)，Q(0,$\frac{4 - 2\sqrt{13}}{9}$)或P(1 + $\sqrt{5}$,-3 + $\sqrt{5}$)，Q(0, -2)。

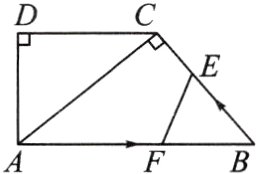
4.如图,在直角梯形ABCD中,AB//DC,∠D =90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/s的速度在线段AB上由A向B匀速运动,E点同时以1cm/s的速度在线段BC上由B向C匀速运动，设运动时间为t秒(0＜t＜5).
　(1)求证:△ACD∽△BAC;
　(2)求DC的长;
　(3)设四边形AFEC的面积为y,求y关于t的函数关系式,并求出y的最小值.
　　　　　　　　　　　　

答案：
(1) 解：因为DC//AB，所以∠BAC = ∠DCA，又AC⊥BC，所以∠ACB = 90°，所以∠D = ∠ACB = 90°，所以△ACD∽△BAC。
(2) 在Rt△ABC中，AC = $\sqrt{AB² - BC²}$ = $\sqrt{10² - 6²}$ = 8cm。因为△ACD∽△BAC，所以$\frac{DC}{AC}=\frac{AC}{AB}$，即$\frac{DC}{8}=\frac{8}{10}$，解得DC = 6.4cm。
(3) 过点E作AB的垂线，垂足为G。因为∠ACB = ∠EGB = 90°，∠B = ∠B，所以△ACB∽△EGB，所以$\frac{EG}{AC}=\frac{BE}{AB}$，即$\frac{EG}{8}=\frac{t}{10}$，故EG = $\frac{4}{5}$tcm。所以y = S△ABC - S△BEF = $\frac{1}{2}$×6×8 - $\frac{1}{2}$(10 - 2t)×$\frac{4}{5}$t = $\frac{4}{5}$t² - 4t + 24 = $\frac{4}{5}$(t - $\frac{5}{2}$)² + 19。故当t = $\frac{5}{2}$时，y有最小值为19cm²。