《2025年名校课堂内外九年级数学下册人教版》

6.(教材第43页第9题变式)
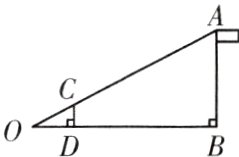
　如图,数学活动小组为了测量学校旗杆AB的高度,使用长为2m的竹竿CD作为测量工具.移动竹竿，使竹竿顶端的影子与旗杆顶端的影子在地面O处重合,测得OD=4m,BD=14m,则旗杆AB的高为______m.

答案： 9

7.如图所示，小明探究视力表的相关内容:当测试距离为5m时，标准视力表中最大的“E"字高度为72.7mm，当测试距离为3m 时，最大的“E"字高度为　　　　　　　(　　　)
　
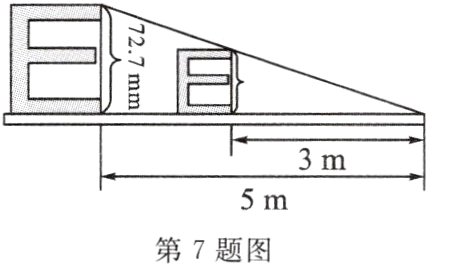
A.121.17mm　　　　B.43.62mm　
C.29.08mm　　　　　D.4.36mm

答案： B

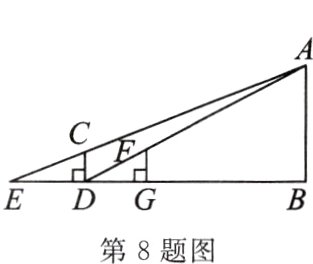
8.(原创题)如图,夜晚路灯下,小莉在点D处测得自己的影长DE=4m,在点G处测得自己的影长DG=3m,E、D、G、B在同一条直线上.已知小莉身高为1.6m,则灯杆AB的高度为________m.

答案： 6.4

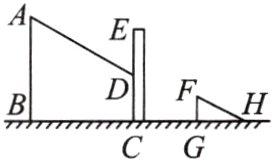
9.如距处离A物在某时刻,1.2m的竹竿FG垂直地面放置，影子GH长为2m,此时树的影子有一部分落在地面上,还有一部分落在建筑物的墙上,墙上的影子CD高为2m,则这棵树的高度为________m.

答案： 4.4

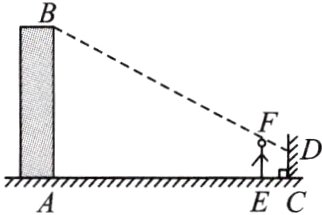
10.小明想利用太阳光测量楼高，他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况，他设计了一种测量方案.具体测量情况如下:如图，小明边移动边观察，发现站到点E处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子高度恰好相同.此时，测得小明落在墙上的影子高度CD=1.2m,CE=0.8一m,CA=30m (A,E,C三点在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB (结果精确到0.1m).
　　　　　　　　　　　

答案： 解：过点D作DG⊥AB于G，交EF于点H，则EH = AG = CD = 1.2m，DH = CE = 0.8m，DG = CA = 30m。
∵EF//AB，
∴△DHF∽△DGB，
∴$\frac{FH}{BG}=\frac{DH}{DG}$，又
∵FH = EF - EH = 1.7 - 1.2 = 0.5(m)，
∴$\frac{0.5}{BG}=\frac{0.8}{30}$，
∴BG = 18.75m，
∴AB = BG + AG = 18.75 + 1.2 = 19.95≈20.0(m)，即楼高AB约为20.0m。

11.(核心素养.推理能力)我军侦察员在距敌方200m的地方发现敌人的一座建筑物，但不知其高度,又不能靠近建筑物，机灵的侦察员立即将食指竖直举在右眼前，闭上左眼，并将食指前后移动，使食指恰好将该建筑物遮住，若食指到眼睛的距离约为40cm,食指的长约为8cm,你能根据上述条件计算出敌方建筑物的高度吗？请你写出计算过程.
　　　　　　　　　　　　

答案：
解：如图所示 ，则MC = 40cm = 0.4m，BC = 8cm = 0.08m，NE = 200m。
∵MC//NE，
∴△AMC∽△ANE，
∴$\frac{AC}{AE}=\frac{MC}{NE}$①，又
∵BC//DE，
∴△ABC∽△ADE，
∴$\frac{BC}{DE}=\frac{AC}{AE}$②，由①、②得$\frac{BC}{DE}=\frac{MC}{NE}$，
∴DE = $\frac{BC\cdot NE}{CM}$ = $\frac{0.08×200}{0.4}$ = 40(m)。答：敌方建筑物高度为40m。