第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
6.如图,△ABC中,AB=AC=18,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=6,求点F到BC的距离.
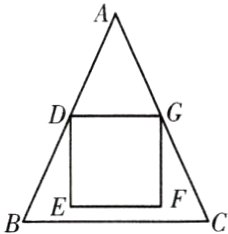

答案:
解:过点A作AM⊥BC于点M,交DG于点N,延长GF交BC于点H.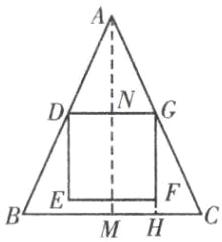
∵AB = AC,AD = AG,
∴AD:AB = AG:AC.
又
∵∠BAC = ∠DAG,
∴△ADG∽△ABC,
∴∠ADG = ∠B,
∴DG//BC.
∵AM⊥BC,
∴AN⊥DG.
∵四边形DEFG是正方形,
∴FG⊥DG,
∴FH⊥BC.
∵AB = AC = 18,BC = 12,AM⊥BC,
∴BM = $\frac{1}{2}$BC = 6,
∴AM = $\sqrt{AB^{2}-BM^{2}} = 12\sqrt{2}$.
∵$\frac{AN}{AM}=\frac{DG}{BC}$,
∴$\frac{AN}{12\sqrt{2}}=\frac{6}{12}$,
∴AN = 6$\sqrt{2}$.
∴MN = AM - AN = 6$\sqrt{2}$.
∴FH = MN - GF = 6$\sqrt{2}$ - 6.
解:过点A作AM⊥BC于点M,交DG于点N,延长GF交BC于点H.

∵AB = AC,AD = AG,
∴AD:AB = AG:AC.
又
∵∠BAC = ∠DAG,
∴△ADG∽△ABC,
∴∠ADG = ∠B,
∴DG//BC.
∵AM⊥BC,
∴AN⊥DG.
∵四边形DEFG是正方形,
∴FG⊥DG,
∴FH⊥BC.
∵AB = AC = 18,BC = 12,AM⊥BC,
∴BM = $\frac{1}{2}$BC = 6,
∴AM = $\sqrt{AB^{2}-BM^{2}} = 12\sqrt{2}$.
∵$\frac{AN}{AM}=\frac{DG}{BC}$,
∴$\frac{AN}{12\sqrt{2}}=\frac{6}{12}$,
∴AN = 6$\sqrt{2}$.
∴MN = AM - AN = 6$\sqrt{2}$.
∴FH = MN - GF = 6$\sqrt{2}$ - 6.
7.有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少毫米?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
(1)如图①,如果原题中要加工的零件是一个矩形,且此矩形由两个并排放置的正方形所组成,此时,这个矩形零件的相邻两条边长又分别为多少毫米?
(2)如图②,如果原题中所要加工的零件只是一个矩形,求这个矩形面积的最大值和达到这个最大值时矩形零件的相邻两条边长.
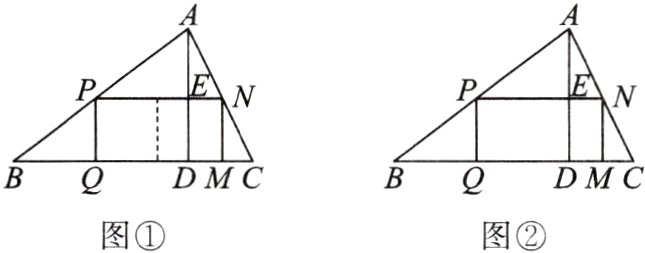
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
(1)如图①,如果原题中要加工的零件是一个矩形,且此矩形由两个并排放置的正方形所组成,此时,这个矩形零件的相邻两条边长又分别为多少毫米?
(2)如图②,如果原题中所要加工的零件只是一个矩形,求这个矩形面积的最大值和达到这个最大值时矩形零件的相邻两条边长.

答案:
(1)解:设矩形的边长PQ = xmm,则PN = 2xmm.
由条件可得△APN∽△ABC.
∴$\frac{PN}{BC}=\frac{AE}{AD}$,
即$\frac{2x}{120}=\frac{80 - x}{80}$,
解得x = $\frac{240}{7}$.
∴PN = $\frac{240}{7}$×2 = $\frac{480}{7}$(mm).
即这个矩形零件的相邻两条边长分别为$\frac{240}{7}$mm,$\frac{480}{7}$mm.
(2)设PN = ymm.
由条件可得△APN∽△ABC,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,
即$\frac{y}{120}=\frac{80 - PQ}{80}$.
解得PQ = 80 - $\frac{2}{3}$y,
∴S矩形PQMN = PN·PQ = y(80 - $\frac{2}{3}$y)= - $\frac{2}{3}$y² + 80y = - $\frac{2}{3}$(y - 60)² + 2400.
∴当y = 60时,S矩形PQMN取得最大值.此时零件的相邻两条边长分别为PN = 60mm,PQ = 80 - $\frac{2}{3}$×60 = 40mm.
(1)解:设矩形的边长PQ = xmm,则PN = 2xmm.
由条件可得△APN∽△ABC.
∴$\frac{PN}{BC}=\frac{AE}{AD}$,
即$\frac{2x}{120}=\frac{80 - x}{80}$,
解得x = $\frac{240}{7}$.
∴PN = $\frac{240}{7}$×2 = $\frac{480}{7}$(mm).
即这个矩形零件的相邻两条边长分别为$\frac{240}{7}$mm,$\frac{480}{7}$mm.
(2)设PN = ymm.
由条件可得△APN∽△ABC,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,
即$\frac{y}{120}=\frac{80 - PQ}{80}$.
解得PQ = 80 - $\frac{2}{3}$y,
∴S矩形PQMN = PN·PQ = y(80 - $\frac{2}{3}$y)= - $\frac{2}{3}$y² + 80y = - $\frac{2}{3}$(y - 60)² + 2400.
∴当y = 60时,S矩形PQMN取得最大值.此时零件的相邻两条边长分别为PN = 60mm,PQ = 80 - $\frac{2}{3}$×60 = 40mm.
查看更多完整答案,请扫码查看


