《2025年名校课堂内外九年级数学下册人教版》

1. 如图,直线y=k₁x + b与双曲线y=$\frac{k₂}{x}$(k₂≠0)相交于A(2,3),B(m,−2)两点.
　(1)求直线和双曲线的解析式;
　(2)点C是x轴正半轴上一点,连接AO,AC,AO = AC,求△AOC的周长.
　　　　　　　　　　　　　

答案： 解:
(1)把A(2,3)代入y=$\frac{k_2}{x}$,得$k_2=2×3=6$.
∴双曲线的解析式为$y=\frac{6}{x}$.
∵B(m,−2)在双曲线上，
∴$-2=\frac{6}{m}$,解得$m = - 3$.
∴B(−3,−2).
把A(2,3),B(−3,−2)代入$y = k_1x + b$,得$\begin{cases}2k_1 + b = 3\\-3k_1 + b = -2\end{cases}$,解得$\begin{cases}k_1 = 1\\b = 1\end{cases}$.
∴直线的解析式为$y = x + 1$.
(2)过点A作AE⊥OC于点E.
∵AO = AC,
∴OE = EC.
∴OC = 2OE = 4.
∵AE = 3,OE = 2,
∴$AO = AC = \sqrt{OE^2 + AE^2}=\sqrt{2^2 + 3^2}=\sqrt{13}$.
∴△AOC的周长为$OA + AC + OC = 4 + 2\sqrt{13}$.

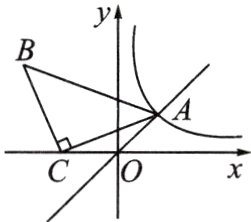
2. (江西省中考)如图,正比例函数y = x的图象与反比例函数y=$\frac{k}{x}$(x＞0)的图象交于点A(1,a),在△ABC中,∠ACB = 90°,CA = CB,点C的坐标为(−2,0).
　(1)求k的值;
　(2)求AB所在直线的解析式.
　　　　　　　　　　　　　　　　　　

答案： 解:
(1)
∵正比例函数$y = x$的图象经过点A(1,a),
∴$a = 1$,
∴A(1,1).
∵点A在反比例函数$y=\frac{k}{x}$(x＞0)的图象上，
∴$k = 1×1 = 1$.
(2)作AD⊥x轴于点D,BE⊥x轴于点E.
∵A(1,1),C(−2,0),
∴AD = 1,CD = 3.
∵∠ACB = 90°,
∴∠ACD + ∠BCE = 90°.
∵∠ACD + ∠CAD = 90°,
∴∠BCE = ∠CAD.
在△BCE和△CAD中，$\begin{cases}∠BEC = ∠CDA = 90°\\∠BCE = ∠CAD\\CB = AC\end{cases}$,
∴△BCE≌△CAD(AAS).
∴CE = AD = 1,BE = CD = 3,
∴B(−3,3).
设直线AB的解析式为$y = mx + n$,
∴$\begin{cases}m + n = 1\\-3m + n = 3\end{cases}$,解得$\begin{cases}m = -\frac{1}{2}\\n = \frac{3}{2}\end{cases}$.
∴直线AB的解析式为$y = -\frac{1}{2}x + \frac{3}{2}$.

3. 如图,在菱形ABOC中,∠A = 60°,它的一个顶点C在反比例函数y=$\frac{k}{x}$的图象上,若菱形的边长为4,则k的值为　　　　　　(　　　)
　　　　　　　
A. 4$\sqrt 3$　　　　　　　B. 2$\sqrt 3$　　　　　　　
C. −4$\sqrt 3$　　　　　　D. −2$\sqrt 3$　　　　　　　　　　　　　　　　　　　

答案： C

4. (陕西省中考)如图,在矩形OABC和正方形CDEF中,点A在y轴正半轴上，点C,F均在x轴正半轴上,点D在边BC上,BC = 2CD,AB = 3.若点B,E在同一个反比例函数的图象上,则这个反比例函数的解析式是__________.
　　　　　　　　　　　　　　　　　　

答案： $y=\frac{18}{x}$