《2025年名校课堂八年级物理3下册沪科版河南专版》

1. 新考向 社会发展 (2024·深圳)“海葵一号”是中国自主设计并建造的亚洲首艘浮式生产储卸型装置，“海葵一号”漂浮在大海上工作，从空中俯瞰像一朵绽放的葵花。傲傲同学查阅资料得知：“海葵一号”的质量是3.7×$10^{7}$ kg，满载时排开海水的质量是1.0×$10^{8}$ kg(g取10 N/kg，海水的密度取1.0×$10^{3}$ kg/${m^{3}}$)。根据已知信息求：
(1)“海葵一号”满载时受到的浮力。
(2)“海葵一号”一次最多能储存石油的质量。
　　　　　　　　　　　　　

答案： 解:
(1)由题可知,“海葵一号”满载时排开海水的重力：$G_{排}=m_{排}g = 1.0×10^{8}\text{ kg}×10\text{ N/kg}=1.0×10^{9}\text{ N}$
根据阿基米德原理，其满载时受到的浮力等于其排开海水的重力，即$F_{浮}=G_{排}=1.0×10^{9}\text{ N}$
(2)“海葵一号”满载漂浮时受到的重力等于排开海水的重力，即其总质量等于排开海水的质量，其一次最多能储存石油的质量：$m_{石油}=m_{排}-m_{0}=1.0×10^{8}\text{ kg}-3.7×10^{7}\text{ kg}=6.3×10^{7}\text{ kg}$

2. (2024·许昌长葛市期末)小亮在学习了“浮力”之后，做了一个观察鸡蛋悬浮的实验，其主要操作步骤如下：
如图所示，先在水平桌面上放置一个底面积为100${cm^{2}}$的圆筒形容器(厚度可忽略)，向容器中注入10 cm深的水，再取一个鸡蛋，称得其质量为55 g，将它轻轻放入水中，发现鸡蛋沉至容器底部，此时测得水面升高了5 mm，然后，向容器中加食盐并不停地搅动，直到鸡蛋恰好悬浮为止(ρ水 = 1.0×$10^{3}$ kg/${m^{3}}$，g取10 N/kg)。
(1)求鸡蛋沉到底部时所受的浮力。
(2)容器中放入鸡蛋时，水对容器底部的压强是多大?
(3)当鸡蛋悬浮时，盐水的密度是多少?
　　　　　　　　　　　　　　　　

答案： 解:
(1)鸡蛋沉至容器底部时，水面上升的高度：$\Delta h = 5\text{ mm}=0.5\text{ cm}$
排开水的体积：$V_{排}=S\Delta h = 100\text{ cm}^{2}×0.5\text{ cm}=50\text{ cm}^{3}=5×10^{-5}\text{ m}^{3}$
此时鸡蛋受到的浮力：$F_{浮}=\rho_{水}gV_{排}=1.0×10^{3}\text{ kg/m}^{3}×10\text{ N/kg}×5×10^{-5}\text{ m}^{3}=0.5\text{ N}$
(2)放入鸡蛋后水面的高度：$h = h_{1}+\Delta h = 10\text{ cm}+0.5\text{ cm}=10.5\text{ cm}=0.105\text{ m}$
水对容器底部的压强：$p=\rho_{水}gh = 1.0×10^{3}\text{ kg/m}^{3}×10\text{ N/kg}×0.105\text{ m}=1.05×10^{3}\text{ Pa}$
(3)因为鸡蛋恰好悬浮，受到的浮力等于鸡蛋的重力，且排开盐水的体积$V_{排}=V_{蛋}=5×10^{-5}\text{ m}^{3}$
由$F_{浮}=\rho_{液}gV_{排}$得盐水的密度：$\rho_{盐水}=\frac{F_{浮}'}{gV_{排}}=\frac{G}{gV_{排}}=\frac{m}{V_{排}}=\frac{0.055\text{ kg}}{5×10^{-5}\text{ m}^{3}}=1.1×10^{3}\text{ kg/m}^{3}$

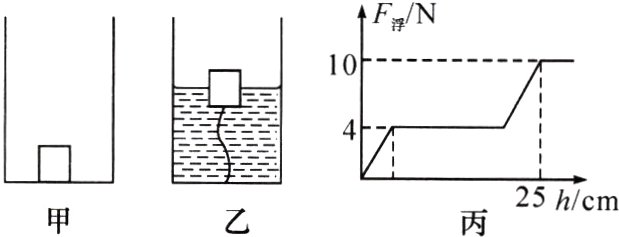
3. (2024·南阳一模)一个棱长为10 cm的立方体木块，细线的一端跟木块底部相连，另一端固定在容器底，如图甲所示(容器高比细线长与木块棱长之和大得多)，现向容器中慢慢加水，如图乙所示。用F浮表示木块受到的浮力，用h表示容器中水的深度。则图丙可以正确描述F浮随深度h变化的关系图像。(g取10 N/kg)
(1)当F浮 = 4 N时，木块处于________(填“漂浮”“悬浮”或“下沉”)状态。
(2)木块的密度为多少?
(3)整个加水过程中，木块只受浮力和重力时，容器中水的深度h变化范围是多少?
　　　　

答案：
(1)漂浮
解:
(2)由$G = mg$得，木块的质量：$m=\frac{G}{g}=\frac{F_{浮}}{g}=\frac{4\text{ N}}{10\text{ N/kg}}=0.4\text{ kg}$
木块体积：$V=(10\text{ cm})^{3}=1000\text{ cm}^{3}=1×10^{-3}\text{ m}^{3}$
木块的密度：$\rho=\frac{m}{V}=\frac{0.4\text{ kg}}{1×10^{-3}\text{ m}^{3}}=0.4×10^{3}\text{ kg/m}^{3}$
(3)当木块刚开始漂浮时，木块只受重力和浮力的作用；由$F_{浮}=\rho_{水}gV_{排}=\rho_{水}gSh$可知，此时水的深度：$h=\frac{F_{浮}}{\rho_{水}gS}=\frac{4\text{ N}}{10^{3}\text{ kg/m}^{3}×10\text{ N/kg}×(0.1\text{ m})^{2}}=0.04\text{ m}=4\text{ cm}$
此时细线的高度为0 cm；由图丙可知，当$h = 25\text{ cm}$时木块恰好浸没，则细线的长度：$L = 25\text{ cm}-10\text{ cm}=15\text{ cm}$
因此细线刚好伸直时水的深度：$h' = 15\text{ cm}+4\text{ cm}=19\text{ cm}$
容器中水的深度变化范围为4~19 cm。