6. 在Rt△ABC中,∠C = 90°,sinA = $\frac{2}{3}$,BC = 6,则AB的长为( )
A. 4
B. 6
C. 8
D. 9
A. 4
B. 6
C. 8
D. 9
答案:
D
7. 如图,菱形ABCD的边长为15,sin∠BAC = $\frac{3}{5}$,则对角线BD的长为______。


答案:
18
8. 如图,已知∠C = 90°,DE⊥AB,垂足为E,若AB = 8,sin∠BDE = $\frac{3}{4}$,则BC的长为______。


答案:
6
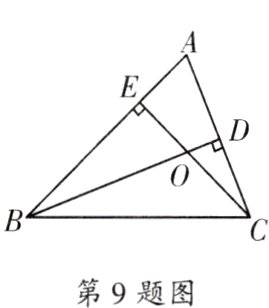
9.(包河区期末)如图,BD⊥AC于点D,CE⊥AB 于点E,BD与CE相交于点O,则图中线段的比不能表示sinA的为( )
A. $\frac{BD}{AB}$
B. $\frac{CD}{OC}$
C. $\frac{AE}{AD}$
D. $\frac{BE}{OB}$

A. $\frac{BD}{AB}$
B. $\frac{CD}{OC}$
C. $\frac{AE}{AD}$
D. $\frac{BE}{OB}$
答案:
C
10.(南充中考)如图,点A,B,C在正方形网格的格点上,则sin∠BAC的值为( )

A. $\frac{\sqrt{2}}{6}$
B. $\frac{\sqrt{26}}{26}$
C. $\frac{\sqrt{26}}{13}$
D. $\frac{\sqrt{13}}{13}$

A. $\frac{\sqrt{2}}{6}$
B. $\frac{\sqrt{26}}{26}$
C. $\frac{\sqrt{26}}{13}$
D. $\frac{\sqrt{13}}{13}$
答案:
B
11.(扬州中考)在△ABC中,∠C = 90°,a,b,c 分别为∠A,∠B,∠C的对边,若b² = ac,则sinA的值为____________。
答案:
$\frac{\sqrt{5}-1}{2}$
12. 如图,已知⊙O的半径为5,弦AB的长为8,P是AB延长线上的一点,BP = 2,求sin∠OPA 的值。


答案:
$\frac{2\sqrt{5}}{5}$或$\frac{2\sqrt{13}}{13}$
13. 如图,在△ABC中,∠C = 90°,BC = 4,AB的垂直平分线MN交AC于点D,且CD:DA = 3:5,求sinA的值。


答案:
解:连接BD,设CD = 3x,则DA = 5x,
又
∵MN垂直平分AB,
∴DB = DA = 5x,
在Rt△BCD中,BC = 4,
∵BD^{2} = CD^{2} + BC^{2},
∴x = 1,
∴AC = 8,
在Rt△ABC中,AB = $\sqrt{BC^{2}+AC^{2}}$ = $\sqrt{4^{2}+8^{2}}$ = 4$\sqrt{5}$,
∴sin A = $\frac{BC}{AB}$ = $\frac{4}{4\sqrt{5}}$ = $\frac{\sqrt{5}}{5}$.
又
∵MN垂直平分AB,
∴DB = DA = 5x,
在Rt△BCD中,BC = 4,
∵BD^{2} = CD^{2} + BC^{2},
∴x = 1,
∴AC = 8,
在Rt△ABC中,AB = $\sqrt{BC^{2}+AC^{2}}$ = $\sqrt{4^{2}+8^{2}}$ = 4$\sqrt{5}$,
∴sin A = $\frac{BC}{AB}$ = $\frac{4}{4\sqrt{5}}$ = $\frac{\sqrt{5}}{5}$.
14. 已知正方形ABCD的边长为4,点Q是直线CD上一点,且DQ = 2,则∠BQC的正弦值为__________________.
答案:
查看更多完整答案,请扫码查看


