1. 三个角分别______,三条边_______的两个三角形相似. 相似用符号“_______”表示,读作“_____”. △ABC与△A'B'C'相似,记作“______”.
答案:
相等 成比例 ∽ 相似于 △ABC∽△A'B'C';
2. 两条直线被一组平行线所截,所得的对应线段_______. 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段______.
答案:
成比例 成比例;
3. 平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形________.
答案:
相似
例1如图,△ABC中,DE//BC,DE = 2,BC = 6,AD = 3. 则BD的长为______.


答案:
6
例2如图,▱ABCD中,点E在边AD的延长线上,连接BE交AC于点G,交CD边于点F,则图中共有______组相似三角形.
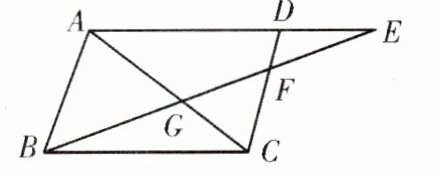

答案:
6
1. 若△ABC∽△A'B'C',BC = 3,B'C' = 1.8,则△A'B'C'与△ABC的相似比为______.
答案:
3:5
2.(核心素养·几何直观)如图,若△ABC∽△DEF,则∠E的度数为______.

答案:
42°
3. 如图,AB//DE,若AC = 4,BC = 2,DC = 1,则EC = ______.

答案:
2
4. 如图,l₁//l₂//l₃,若$\frac{AB}{AC}=\frac{3}{5}$,DE = 6,则EF = ______.

答案:
4
5.(核心素养·模型观念)如图,DE//BC,EC = AD,AE = 2 cm,AB = 7.5 cm,求BD的长.

答案:
解:
∵DE//BC,
∴$\frac{AD}{BD}=\frac{AE}{EC}$.
∵EC=AD,AE=2cm,AB=7.5cm,
∴$\frac{7.5−BD}{BD}=\frac{2}{7.5−BD}$,解得$BD=\frac{25}{2}$(舍)或$BD=\frac{9}{2}$.
∴BD的长为4.5cm.
∵DE//BC,
∴$\frac{AD}{BD}=\frac{AE}{EC}$.
∵EC=AD,AE=2cm,AB=7.5cm,
∴$\frac{7.5−BD}{BD}=\frac{2}{7.5−BD}$,解得$BD=\frac{25}{2}$(舍)或$BD=\frac{9}{2}$.
∴BD的长为4.5cm.
查看更多完整答案,请扫码查看


