《2025年课时掌控九年级数学下册人教版》

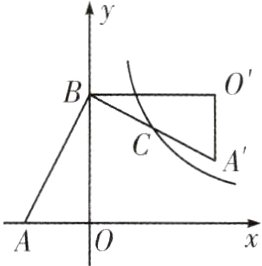
1. 如图，Rt△AOB的两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上，将△AOB绕点B逆时针旋转90°后得到△A'O'B. 若反比例函数$y = \frac{k}{x}$的图象恰好经过斜边A'B的中点C，$S_{\triangle ABO}=4$，$BO = 2AO$，则k的值为____.

答案： 6

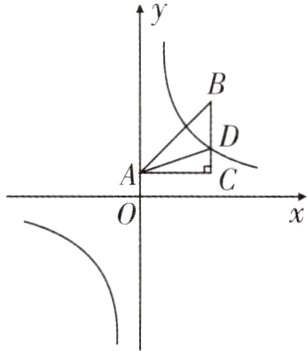
2. 如图，在平面直角坐标系中，O为坐标原点，∠ACB = 90°，A(0,2)，C(6,2). D为等腰直角三角形ABC的边BC上一点，且$S_{\triangle ABC}=3S_{\triangle ADC}$. 反比例函数$y_1 = \frac{k}{x}(k\neq0)$的图象经过点D.
(1)求反比例函数的解析式；
(2)若AB所在直线解析式为$y_2 = ax + b(a\neq0)$，当$y_1＞y_2$时，求x的取值范围.

答案： 解：
(1)
∵$A(0,2)$，$C(6,2)$，
∴$AC = 6$，
由题意得$BC = AC = 6$，$CD = 2$，
∴$D(6,4)$，
∵反比例函数$y_1=\frac{k}{x}(k\neq0)$的图象经过点$D$，
∴$k = 24$，
∴反比例函数的解析式为$y_1=\frac{24}{x}$．
(2)
∵$A(0,2)$，$B(6,8)$，
∴$AB$所在直线的解析式为$y_2 = x + 2$，
联立$\begin{cases}y=\frac{24}{x}\\y=x + 2\end{cases}$，解得$\begin{cases}x=-6\\y=-4\end{cases}$或$\begin{cases}x = 4\\y = 6\end{cases}$，
∴两函数的交点为$(-6,-4)$，$(4,6)$．
∴当$y_1＞y_2$时，$x$的取值范围是$x ＜ -6$或$0 ＜ x ＜ 4$．

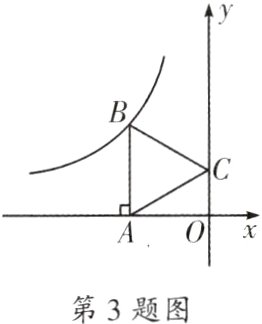
3. 如图，△ABC为等边三角形，点B恰好在反比例函数$y = \frac{k}{x}(k\neq0,x＜0)$的图象上，且BA⊥x轴于点A. 若点C的坐标为(0,1)，则k的值为( )

A. -2$\sqrt{3}$
B. 2$\sqrt{3}$
C. -2
D. 2

答案： A

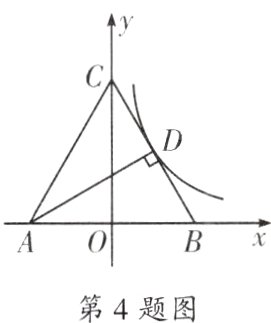
4. 如图，△ABC是等边三角形，点A,B在x轴上，点C在y轴上，AD⊥BC，垂足为D，反比例函数$y = \frac{k}{x}(k＞0)$的图象经过点D，若△ABC的面积为8，则k的值为( )

A. 2
B. $\sqrt{3}$
C. 3
D. 4

答案： A

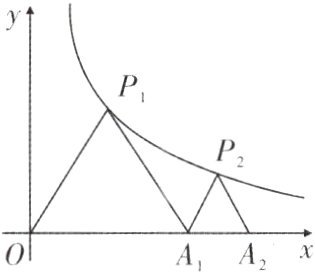
5. 如图，$P_1$是反比例函数$y = \frac{k}{x}(k＞0)$在第一象限图象上的一点，已知△$P_1OA_1$为等边三角形，点$A_1$的坐标为(2,0).
(1)直接写出点$P_1$的坐标为__________；
(2)求此反比例函数的解析式；
(3)若△$P_2A_1A_2$为等边三角形，则点$A_2$的坐标为__________.

答案： 解：
(1)$(1,\sqrt{3})$
(2)反比例函数的解析式为$y=\frac{\sqrt{3}}{x}$．
(3)$(2\sqrt{2},0)$