《2025年课时掌控九年级数学下册人教版》

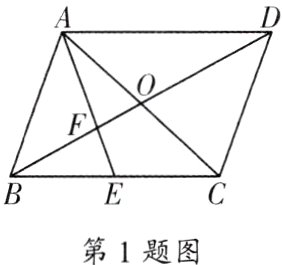
1. 如图,□ABCD的对角线AC,BD相交于点O，E为BC的中点,连接AE交BD于点F. 若OF = 1,则BF的长为（ ）

A. 1.5
B. 2
C. 3
D. 4

答案： B

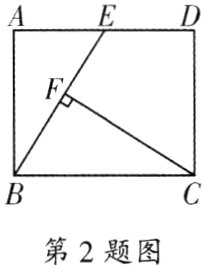
2. 如图,在矩形ABCD中,E是边AD的中点,CF⊥BE,垂足为F,若BF = EF,AE = 1,则AB边的长为（ ）

A. 1
B. $\sqrt{2}$
C. $\sqrt{3}$
D. 2

答案： C

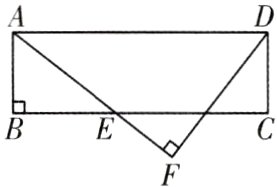
3. 如图,在矩形ABCD中,AB = 3,BC = 10,点E在边BC上,DF⊥AE,垂足为F. 若DF = 6,则线段EF的长为（ ）

A. 2
B. 3
C. 4
D. 5

答案： B

4. 如图,D,E分别是△ABC的边AC,AB上的点,AD = 6,AB = 10,BC = 12,且$\frac{AE}{AC}=\frac{3}{5}$.
(1)求证:△ADE∽△ABC;
(2)求DE的长.

答案：
(1)证明略.
(2)解:
∵△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AE}{AC}$
∵$BC = 12$，$\frac{AE}{AC}=\frac{3}{5}$，
∴$DE=\frac{36}{5}$.

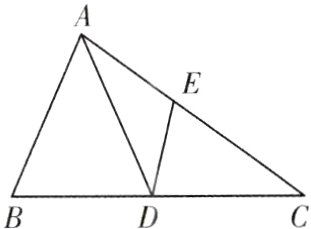
5. 如图,在△ABC中,点D在边BC上,点E在边AC上,且AD = AB,∠DEC = ∠ADB.
(1)求证:△AED∽△ADC;
(2)若AE = 1,EC = 3,求AB的长.

答案：
(1)证明略.
(2)解:
∵△AED∽△ADC,
∴$\frac{AD}{AC}=\frac{AE}{AD}$，即$\frac{AD}{1 + 3}=\frac{1}{AD}$
∴$AD = 2$或$AD = - 2$(舍去). 又
∵$AD = AB$，
∴$AB = 2$.

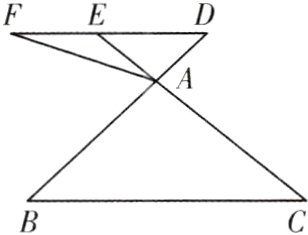
6. (新邵县期末)如图,在△ABC中,D是边BA延长线上一点,过点D作DE//BC,交CA的延长线于点E,F是DE的延长线上一点,连接AF.
(1)如果$\frac{AD}{AB}=\frac{2}{3}$,DE = 6,求边BC的长;
(2)如果∠FAE = ∠B,FA = 6,FE = 4,求DF的长.

答案： 解:
(1)
∵$DE// BC$，
∴△ADE∽△ABC.
∴$\frac{AD}{AB}=\frac{DE}{BC}=\frac{2}{3}$.
∵$DE = 6$，
∴$BC = 9$.
(2)
∵$DE// BC$，
∴$\angle B=\angle D$.
∵$\angle FAE=\angle B$，
∴$\angle FAE=\angle D$.
∵$\angle F=\angle F$，
∴△FAE∽△FDA.
∴$\frac{EF}{FA}=\frac{FA}{DF}$，
∴$DF=\frac{FA^{2}}{EF}=9$.