《2025年亮点给力提优课时作业本四年级数学下册苏教版》

1. 画出下面三角形指定底边上的高。
　　　

答案：
　　　　　　

2. 下图的四个三角形都有一个角被撕掉了，请你将对应的角连起来。
　

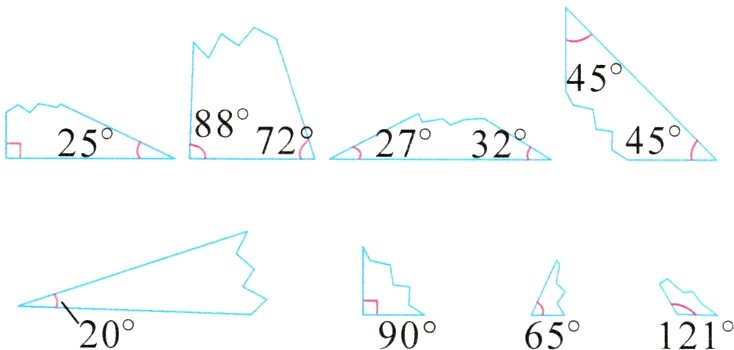
答案：

3. 选一选。
（1）已知一个三角形两条边的长分别是7厘米和8厘米，则第三条边不可能是(　　　)厘米。
A. 2 B. 1 C. 14
（2）亮点原创 全球北极圈内最长的跨海悬索桥由中国工程团队建造，支撑整座大桥的高塔采用两个堆叠的三角形设计，主要是(　　　)。
A. 利用三角形的稳定性
B. 保持对称
C. 节省材料，节省成本

答案： 3.（1）B （2）A

4. 右图中，与三角形ABC同底等高的三角形有(　　　)个；与三角形AEC同底等高的三角形有(　　　)个。
　　　　　　　　

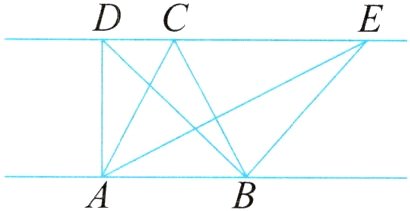
答案： 4. 2 1

5. 小明想做一个三角形的画框。已知其中两条边长分别是35厘米、10厘米，这个三角形画框的周长最短是(　　　)厘米。（长度取整厘米数）

答案： 5. 71

6. 从5根长分别是4厘米、6厘米、8厘米、10厘米、12厘米的小棒中选择3根摆三角形，可以摆出多少种不同的三角形？请一一列举出来。

答案： 6. 可以摆出7种不同的三角形。列举：4厘米、6厘米、8厘米；4厘米、8厘米、10厘米；4厘米、10厘米、12厘米；6厘米、8厘米、10厘米；6厘米、8厘米、12厘米；6厘米、10厘米、12厘米；8厘米、10厘米、12厘米。

7. 一个三角形，最大内角的度数比另外两个内角的度数和大2°，那么这个三角形的最大内角是(　　　)°。

答案： 7. 91 解析：由三角形的内角和是180°，最大内角的度数比另外两个内角的度数和大2°，用解决和差问题的方法，可求出最大内角是(180° + 2°)÷2 = 91°。

8. 如图，在三角形ABC中，∠1=∠2，∠3=∠4，∠5=50°。求∠6的度数。

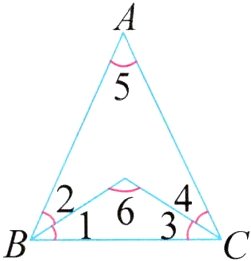
答案：
8. 180° - 50° = 130° 130°÷2 = 65°
∠6 = 180° - 65° = 115°
解析：根据三角形的内角和是180°和∠5 = 50°，可以算出∠1 + ∠2 + ∠3 + ∠4 = 180° - 50° = 130°，又因为∠1 = ∠2，∠3 = ∠4，得到∠1 + ∠3 = 130°÷2 = 65°， ∠6和∠1、∠3在同一个三角形内，根据三角形的内角和是180°，即可算出∠6的度数。