《2025年亮点给力提优课时作业本四年级数学下册苏教版》

1. 在$\square$里填合适的数或字母，在$\bigcirc$里填合适的运算符号。
（1）$99\times99 + 99 = \_\_\times(\_\_\bigcirc\_\_)$
（2）$x\times6 + 94\times\_\_ = x\times(\_\_\bigcirc\_\_)$
（3）$852 - 69 - 31 = \_\_ - (\_\_\bigcirc\_\_)$
（4）$250\times m\times\_\_ = (\_\_\times8)\times\_\_$

答案：
(1) 99 99 + 1
(2) x 6 + 94
(3) 852 69 + 31
(4) 8 250 m

2. （1）已知$M = 99\times101$，$N = 101\times100 - 101$，则$M$与$N$相比，（ ）。
A. $M＞N$
B. $M＜N$
C. $M = N$

答案：
(1) C

（2）在计算$15\times16$时，文文使用的方法是$15\times2\times8$，下面的点子图中，（ ）能体现这种思路。

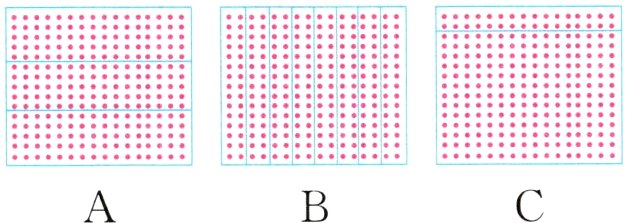
答案：
(2) B

3. 用简便方法计算。
$486 + 158 - 286$ $59\times49 + 49\times41$
$198\times24$ $53\times101 - 53$

答案： 358 4900 4752 5300

4. 丽丽在做题时不小心把$6\times(\_\_ + 2)$错写成了$6\times\_\_ + 2$，她算出的结果与正确的结果相差（ ）。

答案： 10

5. 亮点原创 张浩和爸爸在环形跑道上跑步，环形跑道全长400米，张浩的跑步速度是120米/分。两人从同一起点同时出发，反向而行，2分钟后两人第二次相遇，求爸爸的跑步速度。

答案： 400×2÷2 - 120 = 280(米/分)

6. 兄弟俩绕小区围墙同时同地背向起跑，哥哥每秒跑6米，弟弟每秒跑5米。两人相遇后，弟弟又跑了120秒才回到原出发地，则弟弟绕小区围墙跑一圈要（ ）秒。

答案： 220 解析：由弟弟在两人相遇后又跑了120秒才回到原出发地可知，相遇后弟弟跑的120×5 = 600(米)就是哥哥在相遇前所跑的路程，从而可求出相遇时间为600÷6 = 100(秒)，再加上弟弟后来跑的120秒就是弟弟绕小区围墙跑一圈要用的时间，即100 + 120 = 220(秒)。

7. 小明家和小强家在同一条直线上，两人同时从各自家中出发，相向而行，小明的速度是100米/分，小强的速度是120米/分，两人在距中点80米处相遇。小明和小强两家相距多少米？

答案： 80×2÷(120 - 100) = 8(分) (100 + 120)×8 = 1760(米) 解析：根据“小明的速度是100米/分，小强的速度是120米/分，两人在距中点80米处相遇”可知，相遇时小强比小明多走了2个80米，两人的速度差是120 - 100 = 20(米/分)，所以相遇时两人各走了80×2÷20 = 8(分)，则小明和小强两家相距(100 + 120)×8 = 1760(米)。