第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
7. 如图,AB是⊙O的直径,点C在⊙O上,已知∠A= 35°,则∠B= ______.


答案:
55°
8. 如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,CD= 4,OD= 3,则AB= ______.


答案:
10
9. 如图,点A、F在半圆的直径上,且OA>OF,四边形OABC、ODEF均为矩形. 设AC= m,DF= n,则m、n的大小关系是( ).

A.m>n
B.m<n
C.m= n
D.不确定的

A.m>n
B.m<n
C.m= n
D.不确定的
答案:
C
10. 如图,已知AB、AC是⊙O的两条弦,且AB= AC,∠BOC= 110°. 求∠BAO的度数.


答案:
解:因为AB=AC
在△OAB和△OAC中
$\begin{cases}{OA=OA }\\{OB=OC} \\ { AB=AC } \end{cases}$
所以$△OAB≌△OAC(\mathrm {SSS})$
所以∠AOB=∠AOC
因为∠AOB+∠AOC+∠BOC=360°
∠BOC=110°
所以∠AOB+∠AOC=360°-110°=250°
所以$∠AOB= \frac {1}{2}×250°=125°$
又因为OB=OA
所以∠BAO=∠B
而∠BAO+∠B+∠AOB=180°
所以$∠BAO= \frac {1}{2}(180°-125°)=27.5° $
在△OAB和△OAC中
$\begin{cases}{OA=OA }\\{OB=OC} \\ { AB=AC } \end{cases}$
所以$△OAB≌△OAC(\mathrm {SSS})$
所以∠AOB=∠AOC
因为∠AOB+∠AOC+∠BOC=360°
∠BOC=110°
所以∠AOB+∠AOC=360°-110°=250°
所以$∠AOB= \frac {1}{2}×250°=125°$
又因为OB=OA
所以∠BAO=∠B
而∠BAO+∠B+∠AOB=180°
所以$∠BAO= \frac {1}{2}(180°-125°)=27.5° $
11. 已知点A、B在⊙O内,且画过点A或点B的直径. 下面给出4个结论:① 最多能画1条;② 最多能画2条;③ 最多能画3条;④ 最多能画无数条. 你能画出符合上述哪些结论的已知图形?简单说明这些图形的特征.
答案:
解:①最多能画1条

A、B两点在同一条直径上
②最多能画2条

A、B两点不在同一条直径上,且都不与圆心重合
③最多能画3条
不存在
④最多能画无数条

A、B两个点中只要有一个点与圆心重合即可
解:①最多能画1条

A、B两点在同一条直径上
②最多能画2条

A、B两点不在同一条直径上,且都不与圆心重合
③最多能画3条
不存在
④最多能画无数条

A、B两个点中只要有一个点与圆心重合即可
12. 如图,CD是⊙O的直径,∠EOD= 78°,AE交⊙O于点B,且AB= OE. 求∠E的度数.


答案:
解:连接OB,对图形中的角进行标注,如下图
因为AB=OE,OE=OB
所以AB=OB
所以∠1=∠A
因为OB=OE
所以∠E=∠2=∠1+∠A=2∠A
所以∠EOD=∠E+∠A=3∠A
因为∠EOD=78°
所以∠A=26°
所以∠E=2∠A=26°×2=52°
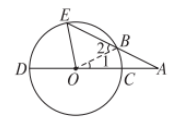
解:连接OB,对图形中的角进行标注,如下图
因为AB=OE,OE=OB
所以AB=OB
所以∠1=∠A
因为OB=OE
所以∠E=∠2=∠1+∠A=2∠A
所以∠EOD=∠E+∠A=3∠A
因为∠EOD=78°
所以∠A=26°
所以∠E=2∠A=26°×2=52°

13. 如图,C、D是⊙O的弦AB上的三等分点,M、N分别是OC、OD的中点. 试说明:AM= BN.


答案:
证明:过O作OE⊥AB于E,则AE=BE
因为C、D是⊙O的弦AB上的三等分点
所以AC=CD=DB
所以AE-AC=BE-DB
所以CE=DE
因为OE⊥CD
所以OC=OD,即△OCD是等腰三角形
所以∠OCD=∠ODC
所以∠ACM=∠BDN
因为M、N为OC、OD的中点
所以CM=DN
在△ACM和△BDN中
$\begin{cases}{AC=BD }\\{∠ACM=∠BDN} \\ {CM=DN } \end{cases}$
所以$△ACM≌△BDN(\mathrm {SAS})$
所以AM=BN
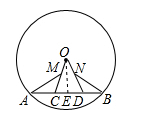
证明:过O作OE⊥AB于E,则AE=BE
因为C、D是⊙O的弦AB上的三等分点
所以AC=CD=DB
所以AE-AC=BE-DB
所以CE=DE
因为OE⊥CD
所以OC=OD,即△OCD是等腰三角形
所以∠OCD=∠ODC
所以∠ACM=∠BDN
因为M、N为OC、OD的中点
所以CM=DN
在△ACM和△BDN中
$\begin{cases}{AC=BD }\\{∠ACM=∠BDN} \\ {CM=DN } \end{cases}$
所以$△ACM≌△BDN(\mathrm {SAS})$
所以AM=BN

查看更多完整答案,请扫码查看


