《2026年金考卷特快专递高中物理》

9. 下列关于光现象描述正确的是

A.海市蜃楼是光的衍射现象
B.光电效应表明光具有粒子性
C.水面上的油膜在阳光下呈现彩色条纹是光的干涉现象
D.斜插在水杯中的筷子看起来像被折断是光的反射现象

答案： 9.BC 光学现象+光电效应 光电效应表明光子具有能量，说明光具有粒子性，B正确；水面上的油膜在阳光下呈现彩色条纹是光的干涉现象，当阳光照在油膜上时，一部分光线会被油膜上表面反射，另一部分光线则会进入油膜内部，被油膜下表面反射，这两部分光相遇时发生干涉现象，C正确。 错误项分析 海市蜃楼是因光的折射和全反射而形成的自然现象【点拨：海市蜃楼现象是在特定条件下，空中或地面出现虚幻的楼台、城郭等景象，这些景象实际上是地球上物体反射的光经过密度不同的大气发生折射和全反射后形成的虚像】，A错误；斜插在水杯中的筷子看起来像被折断是光的折射现象，光从水中斜射入空气中时速度变快，导致传播方向发生改变，而我们的大脑却误以为光是沿直线传来的，从而对物体的位置做出了错误的判断，D错误。

10. 如图所示，理想变压器接在$u =220\sqrt{2} \sin 100\pi t(\mathrm{V})$交流电源上，此时电压表读数为$10 \mathrm{V}$，电流表读数为$4 \mathrm{A}$，电表皆为理想电表，则


A.输入电压有效值为$220 \mathrm{V}$
B.原线圈输入电流为$5.5 \mathrm{A}$
C.滑动变阻器滑片向下滑动，电压表读数减小
D.滑动变阻器滑片向上滑动，电流表读数增大

答案： 10.AD 理想变压器工作原理+电路动态分析+有效值 正弦式交流电的电压最大值是有效值的$\sqrt{2}$倍，则输入电压有效值为U_{1} = \frac{U_{m}}{\sqrt{2}} = 220 V，A正确；由理想变压器的变压规律可知原、副线圈的匝数比为$\frac{n_{1}}{n_{2}} = \frac{U_{1}}{U_{2}} = 22$，由理想变压器的变流规律可得原线圈的输入电流为I_{1} = \frac{n_{2}}{n_{1}}I_{2} \approx 0.18 A，B错误；副线圈两端电压(电压表示数)由输入电压决定，滑动变阻器滑片的滑动不影响电压表读数变化，C错误；滑动变阻器滑片向上滑动，其接入电路的阻值减小，结合C项分析和欧姆定律可知电流表读数增大，D正确。 方法总结 处理理想变压器动态变化问题的思路
(1)原、副线圈匝数比$\frac{n_{1}}{n_{2}}$不变 原线圈 $\frac{U_{1}}{U_{2}} = \frac{n_{1}}{n_{2}} \longrightarrow U_{2}$决定 副线圈 I_{2} = \frac{U_{2}}{R} \longrightarrow 副线圈电流I_{2} 输入功率P_{1} = P_{2}决定 输出功率P_{2} = U_{2}I_{2}决定 原线圈电流I_{1} = \frac{n_{2}}{n_{1}}I_{2}决定
(2)副线圈负载电阻R不变 原线圈 $\frac{U_{1}}{U_{2}} = \frac{n_{1}}{n_{2}} \longrightarrow U_{2}$决定 副线圈电压U_{2} P_{2} = \frac{U_{2}^{2}}{R} \longrightarrow 输出功率P_{2}决定 原线圈 P_{1} = U_{1}I_{1} \longrightarrow 输入功率P_{1}决定

11. 一起重机将质量为$m$的集装箱由静止匀加速竖直向上提升，加速度大小为$a$，匀加速时间为$t$，已知重力加速度大小为$g$，不计空气阻力，则

A.匀加速的最大速度为$at$
B.集装箱的机械能增加$\frac{1}{2}mgat^2$
C.起重机的最大输出功率为$m(g + a)at$
D.起重机对集装箱的作用力大小为$ma$

答案： 11.AC 匀加速直线运动规律+牛顿第二定律+功率+机械能 集装箱由静止做匀加速直线运动，由速度时间公式可知集装箱匀加速的最大速度为$v_{m} = at，$A正确；集装箱运动过程受起重机对其的作用力和重力，由牛顿第二定律可知F - mg = ma，则起重机对集装箱的作用力大小为F = mg + ma = m(g + a)，起重机的最大输出功率为$P_{m} = Fv_{m} = m(g + a)at，$C正确，D错误；一个物体的机械能的变化量等于除重力外其他力对物体做的功，则集装箱的机械能增加量为ΔE = W = Fh，由位移时间公式可知$h = \frac{1}{2}at^{2}，$所以集装箱的机械能增加量为$ΔE = W = \frac{1}{2}m(g + a)at^{2}【$另解：由于机械能包含动能和势能，则集装箱的机械能增加量为$ΔE = mgh + \frac{1}{2}mv_{m}^{2}，$又$h = \frac{1}{2}at^{2}，$$v_{m} = at，$则$ΔE = \frac{1}{2}m(g + a)at^{2}】，$B错误。

12. 如图，足够长的绝缘斜面固定在水平地面上，倾角为$30^{\circ}$，空间有一电场强度大小为$E =\frac{3mg}{2q}$，方向沿斜面向下的匀强电场。质量均为$m$的物块$M$和$N$用绝缘轻绳跨过轻质定滑轮连接，$M$带正电，电荷量为$q$，$N$不带电，并与固定在地面上的竖直轻弹簧连接，弹簧劲度系数为$k$，通过外力控制$M$使轻绳伸直且无拉力，已知重力加速度大小为$g$，不计摩擦，弹簧始终在弹性限度内。现由静止释放$M$，$M$第一次下滑到最低点所用时间为$t$，在此过程中下列说法正确的是


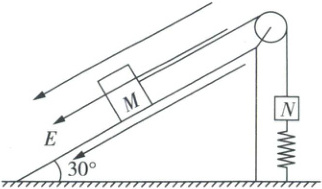
A.释放后瞬间$M$的加速度大小为$2g$
B.$M$的最大速度为$\sqrt{\frac{2mg^2}{k}}$
C.$M$由静止下滑的最大距离为$\frac{3mg}{k}$
D.$M$由静止下滑距离为$\frac{mg}{k}$所用时间为$\frac{t}{3}$

答案： 12.BD 牛顿运动定律+弹簧模型+绳连接体 A项分析：初始时，物块M、N静止，轻绳伸直且无拉力，此时对N由平衡条件可知弹簧弹力大小为T₀ = mg，释放后瞬间轻绳拉力突变，弹簧弹力不变，设轻绳拉力大小为F，则对M、N分别由牛顿第二定律有mgsin 30° + qE - F = ma，F + T₀ - mg = ma，联立解得释放后瞬间M的加速度大小为a = g，A错误； B项分析：M速度最大时，加速度为0，M、N受力平衡，设此时轻绳拉力大小为F'，则有mgsin 30° + qE - F' = 0，kΔx₁ + mg - F' = 0，解得此时弹簧伸长量为$Δx₁ = \frac{mg}{k}，$由A项分析可知释放时弹簧的压缩量为$Δx₀ = \frac{mg}{k}，$则M从释放到其速度最大过程的位移大小为$x₁ = Δx₀ + Δx₁ = \frac{2mg}{k}，$该过程对M、N组成的系统由动能定理有$mgx₁sin 30° + qEx₁ - mgx₁ = \frac{1}{2}×2mv_{m}^{2}，$解得M的最大速度为$v_{m} = \sqrt{\frac{2mg^{2}}{k}}，$B正确； C项分析：以M受力平衡的位置为坐标原点，沿斜面向下为正方向建立x轴，则下滑过程中M偏离平衡位置的位移可用x来表示，设M沿斜面下滑过程中轻绳拉力大小为$F_{绳}，$则对M由牛顿第二定律可得$mgsin 30° + Eq - F_{绳} = ma'，$对N由牛顿第二定律可得$F_{绳} - k(x + \frac{mg}{k}) - mg = ma'，$联立可得下滑过程中M的加速度$a' = - \frac{kx}{2m}，$故下滑过程中M做简谐运动，由B项分析可知M做简谐运动的振幅为$x₁ = \frac{2mg}{k}，$则M由静止下滑的最大距离为$x_{m} = 2x₁ = \frac{4mg}{k}，$C错误； D项分析：从由静止释放M开始计时，下滑过程中，M偏离平衡位置的位移时间关系为$x = - x₁cos\frac{2\pi}{T}t'，$由题意可知简谐运动的周期T = 2t'【点拨：从最高点运动到最低点，M运动了半个周期，所用时间为t'，则简谐运动的周期T = 2t'】，又M下滑距离为$\frac{mg}{k}$时，$x = - \frac{mg}{k} = - \frac{1}{2}x₁，$可得$cos\frac{2\pi}{T}t' = \frac{1}{2}，$又$t' ＜ \frac{T}{2}，$解得$t' = \frac{T}{6} = \frac{t}{3}，$即所用时间为$\frac{t}{3}，$D正确。

13. 某粒子分析器的部分电磁场简化模型如图所示，三维直角坐标系$O − xyz$所在空间中Ⅰ区域($0\leq x\leq d$)存在沿$x$轴正方向的匀强电场(图中未画出)和匀强磁场，磁感应强度大小为$B_1$，Ⅱ区域($d ＜ x\leq 2d$)存在沿$z$轴正方向的匀强磁场，磁感应强度大小为$B_2$，在$x = 2d$处有一足够大的接收屏$P$。原点$O$处的粒子源在$xOz$平面内同时发射带正电的同种粒子甲和乙，甲粒子速度大小为$v_0$，与$x$轴正方向夹角为$30^{\circ}$，乙粒子速度方向与$x$轴正方向夹角为$60^{\circ}$，两粒子沿$x$轴方向速度分量相等。乙粒子以最短时间到达$O_1(d,d,0)$点，进入Ⅱ区域后恰好到达接收屏并被吸收。不计重力及粒子间的相互作用，则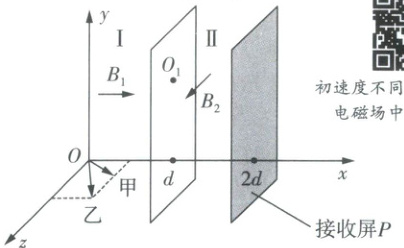


A.两粒子不会同时到达接收屏$P$
B.两个区域磁感应强度大小之比$\frac{B_2}{B_1} =\frac{2}{\pi}-\frac{\sqrt{3}}{6}$
C.乙粒子通过$O_1$点时沿$x$轴方向速度分量$v_x =(\frac{6}{\pi}+\frac{\sqrt{3}}{2})v_0$
D.甲、乙粒子在接收屏$P$上位置的$z$坐标之差$\Delta z =\frac{\pi^2}{12 - \sqrt{3}\pi}d$

答案：
13.BD 带电粒子在电磁复合场中的运动+带电粒子在磁场中的运动 第一步：分析两粒子在I、II区域的运动情况 将两粒子在O点的速度沿x轴方向和z轴方向进行分解，对两粒子进行受力分析可知两粒子在I区域受到沿x轴正方向的电场力和平行于yOz平面的洛伦兹力，则两粒子在I区域的运动可分解为沿x轴正方向的匀加速直线运动和平行于yOz平面的匀速圆周运动，由于发射时两粒子沿x轴方向速度分量相等，且两粒子是同种粒子，则两粒子在I区域运动时沿x轴正方向的运动情况完全一致，故两粒子在I区域的运动时间相同，两粒子同时离开I区域，由于乙粒子以最短时间到达O'(d,d,0)，则乙粒子在平行于yOz平面的匀速圆周运动刚好运动$\frac{1}{2}$周期，又粒子在磁场中的运动周期$T = \frac{2\pi m}{qB}，$则两粒子在平行于yOz平面的匀速圆周运动的周期相同，甲粒子在I区域运动时也刚好在平行于yOz平面内运动$\frac{1}{2}$周期，所以两粒子同时到达接收屏P，A错误。 第二步：根据乙粒子在I区域的具体运动情况判断C项正误 由于发射时两粒子沿x轴方向的速度分量相等，则乙粒子发射时沿x轴方向速度分量为$v_{x0} = v_{0}cos 30° = \frac{\sqrt{3}}{2}v_{0}，$沿z轴方向速度分量为$v_{z0} = v_{0}tan 60° = \frac{3}{2}v_{0}，$根据第一步分析作出乙粒子在I区域的运动轨迹在yOz平面的投影如图1所示，则其圆周运动半径为$r_{z1} = \frac{1}{2}d，$在I区域的运动时间为$t₁ = \frac{1}{2}T₁ = \frac{\pi r_{z1}}{v_{z0}} = \frac{\pi d}{3v_{0}}，$沿x轴方向的运动由匀变速直线运动规律有$d = \frac{1}{2}(v_{x0} + v_{x})t₁，$联立可得乙粒子通过O'点时沿x轴方向速度分量为$v_{x} = (\frac{6}{\pi} - \frac{\sqrt{3}}{2})v_{0}，$C错误。 第三步：结合乙粒子在I、II区域的匀速圆周分运动情况判断B项正误 由于乙粒子进入II区域后恰好到达接收屏，则结合第一步分析作出其在II区域的运动轨迹在xOy平面的投影如图2所示，则该轨迹半径为$r_{z2} = d，$由洛伦兹力提供向心力有$qv_{x}B_{2} = m\frac{v_{x}^{2}}{r_{z2}} $又乙粒子在I区域运动时由洛伦兹力提供向心力有$qv_{z0}B_{1} = m\frac{v_{z0}^{2}}{r_{z1}}，$结合C项分析可知$\frac{B_{2}}{B_{1}} = \frac{2}{\pi} - \frac{\sqrt{3}}{6}，$B正确。 第四步：结合两粒子在I、II区域的匀速圆周分运动情况判断D项正误 发射时甲粒子沿z方向速度分量$v_{z甲} = v_{0}sin 30° = \frac{1}{2}v_{0}，$则甲粒子在II区域沿z轴负方向的分运动速度大小为$v_{z甲} = \frac{1}{2}v_{0}，$由C项分析可知粒子在II区域的运动时间为$t₂ = \frac{1}{4}T₂ = \frac{\pi r_{z2}}{2v_{x}} = \frac{\pi^{2}d}{2(12 - \sqrt{3}\pi)v_{0}}，$则甲、乙粒子在接收屏P上位置的z坐标之差为$Δz = (v_{z乙} - v_{z甲})t₂ = \frac{\pi^{2}}{12 - \sqrt{3}\pi}d，$D正确。 考情速递 三维空间思维成高分关键分水岭 高考试题为了提升难度，往往将二维平面的运动向三维空间拓展，比如2025陕西卷第14题考查电子在空间磁场中的运动；2025山东卷第8题考查空间内的受力分析，第10题考查空间内的曲线运动，这些试题都是典型的三维空间的问题。本题延续这一特点，考查两不同初速度的粒子在电磁复合场中的运动对比，对考生的空间想象能力要求很高。考生遇到这类问题时，一般可将三维空间问题转化成二维平面问题解决，在平时备考时，可针对性训练该类题目，锻炼空间想象力，提升考生解决问题的能力。