2026年金考卷特快专递高中物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷特快专递高中物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
15. (14分)精密条纹相机通过将时域信号转换成空间信息可实现超短激光脉冲持续时间的测量,其简化原理如图所示。某个待测激光脉冲的持续时间为$\Delta t$,经过狭缝和聚焦透镜入射至真空条纹管的光电阴极中心。由于光电效应,产生与输入激光脉冲持续时间相同的电子脉冲。电子脉冲先后经加速和偏转等过程打到荧光屏上。阳极与光电阴极间的加速电压为$U_1$,距离为$d_1$。偏转极板间距和长度分别为$d_2$和$L_2$,其左端与阳极的距离为$L_1$,右端与荧光屏的距离为$L_3$。光电效应产生电子的初速度忽略不计,电子不会打到偏转极板上。电子质量为$m$,电荷量大小为$e$,不考虑电子重力和相对论效应,以及电子之间相互作用。所有元件的中心在同一条直线上,并以荧光屏中心$O$为原点、竖直方向为$y$轴建立坐标系。(普朗克常量$h=6.63×10^{-34}$ J·s,光速$c=3×10^8$ m/s)
(1)现有多碱、Au和CsI三种常用的光电阴极材料,它们的逸出功分别约为1.1 eV、4.5 eV、6.2 eV。若要使波长范围为200~900 nm的入射激光都能打出光电子,请通过定量分析确定应选用哪种光电阴极材料。(1 eV=$1.6×10^{-19}$ J)
(2)当偏转极板间电压$U$为常量时,求电子打在荧光屏上的位置。
(3)真实情况下,偏转极板间电压$U$与时间$t$的关系为$U=U_0+kt$($U_0$和$k$为大于零的常量),其零时刻与激光脉冲刚入射至光电阴极的时刻相同。
①求最后进入偏转极板间的电子离开偏转极板时$y$方向速度的大小;
②若$L_2$很小且$L_2\ll L_3$,此时可忽略不同时刻电子在偏转极板间$y$方向位移的差别,求电子脉冲在荧光屏上的空间宽度$\Delta y$与激光脉冲持续时间$\Delta t$的关系。
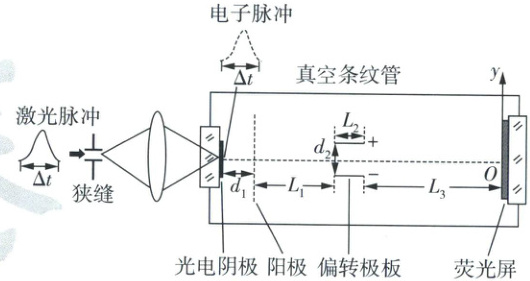
精密条纹相机如何测量超短激光脉冲持续时间?
(1)现有多碱、Au和CsI三种常用的光电阴极材料,它们的逸出功分别约为1.1 eV、4.5 eV、6.2 eV。若要使波长范围为200~900 nm的入射激光都能打出光电子,请通过定量分析确定应选用哪种光电阴极材料。(1 eV=$1.6×10^{-19}$ J)
(2)当偏转极板间电压$U$为常量时,求电子打在荧光屏上的位置。
(3)真实情况下,偏转极板间电压$U$与时间$t$的关系为$U=U_0+kt$($U_0$和$k$为大于零的常量),其零时刻与激光脉冲刚入射至光电阴极的时刻相同。
①求最后进入偏转极板间的电子离开偏转极板时$y$方向速度的大小;
②若$L_2$很小且$L_2\ll L_3$,此时可忽略不同时刻电子在偏转极板间$y$方向位移的差别,求电子脉冲在荧光屏上的空间宽度$\Delta y$与激光脉冲持续时间$\Delta t$的关系。

精密条纹相机如何测量超短激光脉冲持续时间?
答案:
15
(1)结合$E = h\nu$和$\nu = \frac{c}{\lambda}$可知波长为$\lambda$的入射激光的光子能量为$E = h\frac{c}{\lambda}$ ………………………… (1分)
根据入射激光的波长范围可知入射激光的光子能量范围为1.4~6.2eV
由光电效应的条件可知,要使入射激光的光子能量都大于阴极材料的逸出功,则要选用的光电阴极材料的逸出功要小于1.4eV,由于只有多碱的逸出功小于1.4eV,则应选用的光电阴极材料为多碱阴极材料 ………………………… (2分)
(2)光电效应产生电子的初速度忽略不计,电子从光电阴极运动到偏转极板左端竖直边缘线的过程,由动能定理有$eU_1 = \frac{1}{2}mv_0^2$ ………………………… (1分)
解得电子进入偏转极板间的速度大小为$v_0 = \sqrt{\frac{2eU_1}{m}}$
电子在偏转极板间所受电场力沿y轴正方向,则其在偏转极板间做类平抛运动,向y轴正方向偏转,电子在水平方向做匀速直线运动,可知电子在偏转极板间的运动时间为$t_1 = \frac{L_2}{v_0} = L_2\sqrt{\frac{m}{2eU_1}}$ ………………………… (1分)
沿y轴正方向有$y_1 = \frac{1}{2} · \frac{eU}{md_2}t_1^2$ ………………………… (1分)
解得$y_1 = \frac{UL_2^2}{4U_1d_2}$
电子离开偏转极板时的速度沿y轴分量的大小为$v_{y1} = \frac{eU}{md_2}t_1$ ………………………… (1分)
电子从离开偏转极板到打到荧光屏上的过程做匀速直线运动,速度方向与水平方向的夹角的正切值为$\frac{v_{y1}}{v_0}$
则电子从离开偏转极板到打到荧光屏上的时间内在y轴方向的位移为$y_2 = L_3 · \frac{v_{y1}}{v_0} = \frac{UL_2L_3}{2U_1d_2}$ ………………………… (1分)
因此电子打在荧光屏上的位置为$y = y_1 + y_2 = \frac{UL_2(L_2 + 2L_3)}{4U_1d_2}$ ………………………… (2分)
(3)①电子在光电阴极与阳极间做匀加速直线运动,该过程结合牛顿第二定律和位移时间公式有$d_1 = \frac{1}{2} · \frac{eU_1}{md_1}t_1^2$ ………………………… (1分)
电子在阳极与偏转极板左端竖直边缘线间做匀速直线运动,则电子从光电阴极运动到偏转极板左端竖直边缘线的时间为$t_3 = t_2 + \frac{L_1}{2v_0} = (d_1 + \frac{L_1}{2})\sqrt{\frac{2m}{eU_1}}$
最后进入偏转极板间的电子进入偏转极板间时偏转极板间的电压为$U_1' = U_0 + k(t_3 + \Delta t)$,离开偏转极板间时偏转极板间的电压为$U_2' = U_1' + k\Delta t$
由牛顿第二定律可知电子在偏转极板间的加速度为$a_p = \frac{eU}{md_2}$,U随时间均匀变化,则$a_p$随时间t均匀变化,又$a_p - t$图像与坐标轴围成图形的面积表示电子沿y轴方向速度变化量,故最后进入偏转极板间的电子离开偏转极板时y方向的速度大小为$v_{y2} = \frac{1}{2}(a_p + a_{p2})t_1 = \frac{e}{2md_2}(U_1' + U_2')t_1 = (U_0 + k\Delta t)\frac{L_2}{d_2}\sqrt{\frac{e}{2mU_1}} + \frac{kL_2}{4U_1d_2}(4d_1 + 2L_1 + L_2)$ ………………………… (1分)
②由①问分析可知最先进入偏转极板间的电子与最后进入偏转极板间的电子离开偏转极板时y轴方向的速度差为$\Delta v_y = \frac{kL_2}{d_2}\sqrt{\frac{e}{2mU_1}} \Delta t$ ………………………… (1分)
则电子脉冲在荧光屏上的空间宽度$\Delta y = \frac{L_3}{v_0} · \Delta v_y$,即$\Delta y$与$\Delta t$的关系为$\Delta y = \frac{kL_2L_3}{2U_1d_2} \Delta t$ ………………………… (1分)
考情速递 原子物理与电磁学的跨模块综合考查已成常态
近几年高考趋向于跨模块知识的考查,尤其钟爱原子物理与电磁学的跨模块综合,比如2025年1月浙江卷第18题将衰变与离子在电磁场中的运动综合,2025年6月浙江卷第18题将核反应与磁偏转系统相结合,2017年北京卷第23题将原子物理中的衰变与带电粒子在磁场中的运动进行融合,2016年上海卷第10题将原子物理与带电粒子在电场中的偏转进行融合。
本题延续这一特点,将光电效应与电子在电场中的运动结合,综合原子物理与电场的知识,考查考生对经典模型与基础知识的掌握,以及知识间的融会贯通。考生在备考时可以多接触跨模块综合类的题目,提升解决问题的能力。
(1)结合$E = h\nu$和$\nu = \frac{c}{\lambda}$可知波长为$\lambda$的入射激光的光子能量为$E = h\frac{c}{\lambda}$ ………………………… (1分)
根据入射激光的波长范围可知入射激光的光子能量范围为1.4~6.2eV
由光电效应的条件可知,要使入射激光的光子能量都大于阴极材料的逸出功,则要选用的光电阴极材料的逸出功要小于1.4eV,由于只有多碱的逸出功小于1.4eV,则应选用的光电阴极材料为多碱阴极材料 ………………………… (2分)
(2)光电效应产生电子的初速度忽略不计,电子从光电阴极运动到偏转极板左端竖直边缘线的过程,由动能定理有$eU_1 = \frac{1}{2}mv_0^2$ ………………………… (1分)
解得电子进入偏转极板间的速度大小为$v_0 = \sqrt{\frac{2eU_1}{m}}$
电子在偏转极板间所受电场力沿y轴正方向,则其在偏转极板间做类平抛运动,向y轴正方向偏转,电子在水平方向做匀速直线运动,可知电子在偏转极板间的运动时间为$t_1 = \frac{L_2}{v_0} = L_2\sqrt{\frac{m}{2eU_1}}$ ………………………… (1分)
沿y轴正方向有$y_1 = \frac{1}{2} · \frac{eU}{md_2}t_1^2$ ………………………… (1分)
解得$y_1 = \frac{UL_2^2}{4U_1d_2}$
电子离开偏转极板时的速度沿y轴分量的大小为$v_{y1} = \frac{eU}{md_2}t_1$ ………………………… (1分)
电子从离开偏转极板到打到荧光屏上的过程做匀速直线运动,速度方向与水平方向的夹角的正切值为$\frac{v_{y1}}{v_0}$
则电子从离开偏转极板到打到荧光屏上的时间内在y轴方向的位移为$y_2 = L_3 · \frac{v_{y1}}{v_0} = \frac{UL_2L_3}{2U_1d_2}$ ………………………… (1分)
因此电子打在荧光屏上的位置为$y = y_1 + y_2 = \frac{UL_2(L_2 + 2L_3)}{4U_1d_2}$ ………………………… (2分)
(3)①电子在光电阴极与阳极间做匀加速直线运动,该过程结合牛顿第二定律和位移时间公式有$d_1 = \frac{1}{2} · \frac{eU_1}{md_1}t_1^2$ ………………………… (1分)
电子在阳极与偏转极板左端竖直边缘线间做匀速直线运动,则电子从光电阴极运动到偏转极板左端竖直边缘线的时间为$t_3 = t_2 + \frac{L_1}{2v_0} = (d_1 + \frac{L_1}{2})\sqrt{\frac{2m}{eU_1}}$
最后进入偏转极板间的电子进入偏转极板间时偏转极板间的电压为$U_1' = U_0 + k(t_3 + \Delta t)$,离开偏转极板间时偏转极板间的电压为$U_2' = U_1' + k\Delta t$
由牛顿第二定律可知电子在偏转极板间的加速度为$a_p = \frac{eU}{md_2}$,U随时间均匀变化,则$a_p$随时间t均匀变化,又$a_p - t$图像与坐标轴围成图形的面积表示电子沿y轴方向速度变化量,故最后进入偏转极板间的电子离开偏转极板时y方向的速度大小为$v_{y2} = \frac{1}{2}(a_p + a_{p2})t_1 = \frac{e}{2md_2}(U_1' + U_2')t_1 = (U_0 + k\Delta t)\frac{L_2}{d_2}\sqrt{\frac{e}{2mU_1}} + \frac{kL_2}{4U_1d_2}(4d_1 + 2L_1 + L_2)$ ………………………… (1分)
②由①问分析可知最先进入偏转极板间的电子与最后进入偏转极板间的电子离开偏转极板时y轴方向的速度差为$\Delta v_y = \frac{kL_2}{d_2}\sqrt{\frac{e}{2mU_1}} \Delta t$ ………………………… (1分)
则电子脉冲在荧光屏上的空间宽度$\Delta y = \frac{L_3}{v_0} · \Delta v_y$,即$\Delta y$与$\Delta t$的关系为$\Delta y = \frac{kL_2L_3}{2U_1d_2} \Delta t$ ………………………… (1分)
考情速递 原子物理与电磁学的跨模块综合考查已成常态
近几年高考趋向于跨模块知识的考查,尤其钟爱原子物理与电磁学的跨模块综合,比如2025年1月浙江卷第18题将衰变与离子在电磁场中的运动综合,2025年6月浙江卷第18题将核反应与磁偏转系统相结合,2017年北京卷第23题将原子物理中的衰变与带电粒子在磁场中的运动进行融合,2016年上海卷第10题将原子物理与带电粒子在电场中的偏转进行融合。
本题延续这一特点,将光电效应与电子在电场中的运动结合,综合原子物理与电场的知识,考查考生对经典模型与基础知识的掌握,以及知识间的融会贯通。考生在备考时可以多接触跨模块综合类的题目,提升解决问题的能力。
查看更多完整答案,请扫码查看


