2026年金考卷特快专递高中物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷特快专递高中物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. (8 分)某兴趣小组利用打点计时器测量小车运动的速度和加速度。
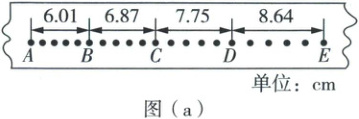
(1)甲同学某次测量时所用的纸带的一部分如图 (a) 所示,打点计时器电源频率为$50\ Hz$,则打下$C$点时小车的速度大小$v_C =$
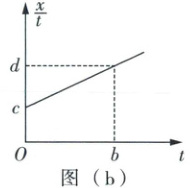
(2)乙同学通过多次操作从其中选择了一条比较清晰的纸带,并选取了一个比较清晰的点为计数点 0,依次计算出其他计数点到 0 点的距离$x$与所用时间$t$的比值$\frac{x}{t}$,作出$\frac{x}{t}-t$的图像,如图 (b) 所示,坐标系中已标出的坐标值为已知量,则打下 0 点时小车的速度大小$v_0 =$
(1)甲同学某次测量时所用的纸带的一部分如图 (a) 所示,打点计时器电源频率为$50\ Hz$,则打下$C$点时小车的速度大小$v_C =$
0.73
$ m/s$;小车的加速度大小$a_0 =$0.88
$ m/s^2$。(结果均保留 2 位有效数字)
(2)乙同学通过多次操作从其中选择了一条比较清晰的纸带,并选取了一个比较清晰的点为计数点 0,依次计算出其他计数点到 0 点的距离$x$与所用时间$t$的比值$\frac{x}{t}$,作出$\frac{x}{t}-t$的图像,如图 (b) 所示,坐标系中已标出的坐标值为已知量,则打下 0 点时小车的速度大小$v_0 =$
c
,小车的加速度大小$a =$$\frac{2(d - c)}{b}$
。(均用$b$、$c$、$d$表示)
答案:
11.
(1)$0.73(2$分) $0.88(2$分)
(2)c(2分) $\frac{2(d - c)}{b}(2$分)
测量小车运动的速度和加速度+实验原理+数据处理
(1) 由题可知打点计时器的打点周期$T_{0} = \frac{1}{f} = \frac{1}{50}s = 0.02s$,由题图(a)可知打下相邻两个计数点间的时间间隔为$\Delta T = 5T_{0} = 0.1s$,根据匀变速直线运动中某段时间的平均速度等于该段时间中间时刻的瞬时速度可知,打下C点时小车的速度大小$v_{C} = \frac{x_{BC} + x_{CD}}{2\Delta T} = 0.73m/s$;根据逐差法$\Delta x = aT^{2}$得小车的加速度大小$a_{0} = \frac{x_{CE} - x_{AC}}{(2\Delta T)^{2}} = 0.88m/s^{2}$。
(2) 根据匀加速直线运动位移时间公式$x = v_{0}t + \frac{1}{2}at^{2}$可得$\frac{x}{t} = v_{0} + \frac{1}{2}at$,则$\frac{x}{t} - t$图像的斜率表示$\frac{a}{2}$,纵截距表示$v_{0}$,由题图(b)可知小车打下O点时的速度大小$v_{0} = c$,小车的加速度大小$a = 2k = \frac{2(d - c)}{b}$。
(1)$0.73(2$分) $0.88(2$分)
(2)c(2分) $\frac{2(d - c)}{b}(2$分)
测量小车运动的速度和加速度+实验原理+数据处理
(1) 由题可知打点计时器的打点周期$T_{0} = \frac{1}{f} = \frac{1}{50}s = 0.02s$,由题图(a)可知打下相邻两个计数点间的时间间隔为$\Delta T = 5T_{0} = 0.1s$,根据匀变速直线运动中某段时间的平均速度等于该段时间中间时刻的瞬时速度可知,打下C点时小车的速度大小$v_{C} = \frac{x_{BC} + x_{CD}}{2\Delta T} = 0.73m/s$;根据逐差法$\Delta x = aT^{2}$得小车的加速度大小$a_{0} = \frac{x_{CE} - x_{AC}}{(2\Delta T)^{2}} = 0.88m/s^{2}$。
(2) 根据匀加速直线运动位移时间公式$x = v_{0}t + \frac{1}{2}at^{2}$可得$\frac{x}{t} = v_{0} + \frac{1}{2}at$,则$\frac{x}{t} - t$图像的斜率表示$\frac{a}{2}$,纵截距表示$v_{0}$,由题图(b)可知小车打下O点时的速度大小$v_{0} = c$,小车的加速度大小$a = 2k = \frac{2(d - c)}{b}$。
12. (8 分)某实验小组探究滑块在气垫导轨上运动规律的实验装置如图甲所示,实验步骤如下:
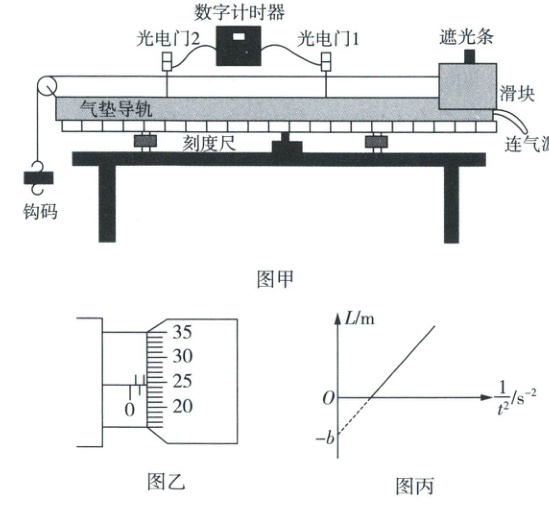
a. 将一端带有定滑轮的气垫导轨放置于水平桌面上,调节气垫导轨水平;
b. 在气垫导轨上安装光电门 1 和 2,将光电门 1 固定;
c. 测出遮光条的宽度$d$如图乙所示,将遮光条安装在滑块上,测出滑块和遮光条的总质量$M$;
d. 用细线连接滑块,将滑块放置在光电门 1 右侧气垫导轨上的某一位置,细线绕过左侧的定滑轮,悬挂质量为$m$的钩码,调节细线与导轨平行;
e. 启动气源,气垫导轨正常工作后,由静止释放滑块,记录遮光条通过光电门 1 的遮光时间$t_0$和通过光电门 2 的遮光时间$t$;
f. 改变光电门 2 的位置,保持滑块从同一位置静止释放,多次记录遮光条通过光电门 2 的遮光时间$t$和光电门 1、2 的间距$L$,作出$L-\frac{1}{t^2}$图像如图丙所示。
(1)遮光条的宽度$d =$
(2)滑块在导轨上滑动时的加速度大小$a =$
(3)若图丙中图像的斜率为$k$,纵截距为$-b$,重力加速度大小为$g$,则遮光条通过光电门 1 的瞬时速度为$v_1 =$

a. 将一端带有定滑轮的气垫导轨放置于水平桌面上,调节气垫导轨水平;
b. 在气垫导轨上安装光电门 1 和 2,将光电门 1 固定;
c. 测出遮光条的宽度$d$如图乙所示,将遮光条安装在滑块上,测出滑块和遮光条的总质量$M$;
d. 用细线连接滑块,将滑块放置在光电门 1 右侧气垫导轨上的某一位置,细线绕过左侧的定滑轮,悬挂质量为$m$的钩码,调节细线与导轨平行;
e. 启动气源,气垫导轨正常工作后,由静止释放滑块,记录遮光条通过光电门 1 的遮光时间$t_0$和通过光电门 2 的遮光时间$t$;
f. 改变光电门 2 的位置,保持滑块从同一位置静止释放,多次记录遮光条通过光电门 2 的遮光时间$t$和光电门 1、2 的间距$L$,作出$L-\frac{1}{t^2}$图像如图丙所示。
(1)遮光条的宽度$d =$
1.745
$ mm$。(2)滑块在导轨上滑动时的加速度大小$a =$
$\frac{d^{2}}{2L}(\frac{1}{t^{2}_{2}} - \frac{1}{t^{2}_{1}})$
。(用$d$、$t$、$t_0$、$L$表示)(3)若图丙中图像的斜率为$k$,纵截距为$-b$,重力加速度大小为$g$,则遮光条通过光电门 1 的瞬时速度为$v_1 =$
$d\sqrt{\frac{b}{k}}$
,$\frac{m}{M} =$$\frac{d^{2}}{2kg - d^{2}}$
。(均从$b$、$d$、$k$、$g$中选用合适的字母表示)
答案:
12.
(1)$1.745(1.743 ∼ 1.747$均可,$2$分)
(2)$\frac{d^{2}}{2L}(\frac{1}{t^{2}_{2}} - \frac{1}{t^{2}_{1}})(2$分)
(3)$d\sqrt{\frac{b}{k}}(2$分) $\frac{d^{2}}{2kg - d^{2}}(2$分)
实验攻略
(1) 熟练掌握螺旋测微器的读数规则即可写出遮光条的宽度。
(2) 根据遮光条经过光电门的遮光时间可表示出滑块经过光电门的速度,根据匀变速直线运动速度位移公式即可求解滑块在导轨上滑动时的加速度大小。
(3) 对钩码、滑块和遮光条整体由动能定理得出L、$\frac{1}{t^{2}}$关系式,利用数形结合法分析出$L - \frac{1}{t^{2}}$图像斜率、纵截距的物理意义即可求解$t_{0}$、$\frac{m}{M}$,进而根据$v_{1} = \frac{d}{t_{0}}$求解遮光条经过光电门1的瞬时速度。
探究滑块在气垫导轨上的运动规律+螺旋测微器的读数+实验原理+数据处理
(1) 螺旋测微器的读数方法是固定刻度读数+可动刻度读数,则遮光条的宽度$d = 1.5mm + 24.5 × 0.01mm = 1.745mm$。
(2) 遮光条宽度很小,通过光电门的时间很短,根据极短时间内的平均速度近似等于瞬时速度可知,滑块经光电门1的速度大小为$v_{1} = \frac{d}{t_{0}}$,滑块经光电门2的速度大小为$v_{2} = \frac{d}{t}$,根据匀变速直线运动的速度位移公式$v^{2}_{2} - v^{2}_{1} = 2aL$,可知滑块在导轨上滑动的加速度大小为$a = \frac{(\frac{d}{t})^{2} - (\frac{d}{t_{0}})^{2}}{2L} = \frac{d^{2}}{2L}(\frac{1}{t^{2}} - \frac{1}{t^{2}_{0}})$。
(3) 对钩码、滑块和遮光条由动能定理有$mgL = \frac{1}{2}(m + M)v^{2}_{2} - \frac{1}{2}(m + M)v^{2}_{1}$,可得$L = \frac{(m + M)d^{2}}{2mg}\frac{1}{t^{2}} - \frac{(m + M)d^{2}}{2mgt^{2}_{0}}$,则$L - \frac{1}{t^{2}}$图像的斜率表示$\frac{(m + M)d^{2}}{2mg}$,纵截距表示$- \frac{(m + M)d^{2}}{2mgt^{2}_{0}}$,根据题图丙可知,$k = \frac{(m + M)d^{2}}{2mg}$,$b = - \frac{(m + M)d^{2}}{2mgt^{2}_{0}}$,解得$t_{0} = \sqrt{\frac{k}{b}}\frac{m}{M} = \frac{d^{2}}{2kg - d^{2}}$,根据$v_{1} = \frac{d}{t_{0}}$可得$v_{1} = d\sqrt{\frac{b}{k}}$。
(1)$1.745(1.743 ∼ 1.747$均可,$2$分)
(2)$\frac{d^{2}}{2L}(\frac{1}{t^{2}_{2}} - \frac{1}{t^{2}_{1}})(2$分)
(3)$d\sqrt{\frac{b}{k}}(2$分) $\frac{d^{2}}{2kg - d^{2}}(2$分)
实验攻略
(1) 熟练掌握螺旋测微器的读数规则即可写出遮光条的宽度。
(2) 根据遮光条经过光电门的遮光时间可表示出滑块经过光电门的速度,根据匀变速直线运动速度位移公式即可求解滑块在导轨上滑动时的加速度大小。
(3) 对钩码、滑块和遮光条整体由动能定理得出L、$\frac{1}{t^{2}}$关系式,利用数形结合法分析出$L - \frac{1}{t^{2}}$图像斜率、纵截距的物理意义即可求解$t_{0}$、$\frac{m}{M}$,进而根据$v_{1} = \frac{d}{t_{0}}$求解遮光条经过光电门1的瞬时速度。
探究滑块在气垫导轨上的运动规律+螺旋测微器的读数+实验原理+数据处理
(1) 螺旋测微器的读数方法是固定刻度读数+可动刻度读数,则遮光条的宽度$d = 1.5mm + 24.5 × 0.01mm = 1.745mm$。
(2) 遮光条宽度很小,通过光电门的时间很短,根据极短时间内的平均速度近似等于瞬时速度可知,滑块经光电门1的速度大小为$v_{1} = \frac{d}{t_{0}}$,滑块经光电门2的速度大小为$v_{2} = \frac{d}{t}$,根据匀变速直线运动的速度位移公式$v^{2}_{2} - v^{2}_{1} = 2aL$,可知滑块在导轨上滑动的加速度大小为$a = \frac{(\frac{d}{t})^{2} - (\frac{d}{t_{0}})^{2}}{2L} = \frac{d^{2}}{2L}(\frac{1}{t^{2}} - \frac{1}{t^{2}_{0}})$。
(3) 对钩码、滑块和遮光条由动能定理有$mgL = \frac{1}{2}(m + M)v^{2}_{2} - \frac{1}{2}(m + M)v^{2}_{1}$,可得$L = \frac{(m + M)d^{2}}{2mg}\frac{1}{t^{2}} - \frac{(m + M)d^{2}}{2mgt^{2}_{0}}$,则$L - \frac{1}{t^{2}}$图像的斜率表示$\frac{(m + M)d^{2}}{2mg}$,纵截距表示$- \frac{(m + M)d^{2}}{2mgt^{2}_{0}}$,根据题图丙可知,$k = \frac{(m + M)d^{2}}{2mg}$,$b = - \frac{(m + M)d^{2}}{2mgt^{2}_{0}}$,解得$t_{0} = \sqrt{\frac{k}{b}}\frac{m}{M} = \frac{d^{2}}{2kg - d^{2}}$,根据$v_{1} = \frac{d}{t_{0}}$可得$v_{1} = d\sqrt{\frac{b}{k}}$。
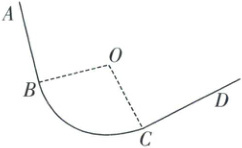
13. ☆(10 分)如图所示,一段水平的公路由两直道$AB$、$CD$以及圆弧弯道$BC$组成。一辆汽车在$AB$段上以$v_0 = 72\ km/h$的速率匀速行驶,接近弯道时以大小为$a_1 = 4\ m/s^2$的加速度匀减速刹车,然后以不发生侧滑的最大速率通过圆弧弯道。进入$CD$后以$a_2 = 2\ m/s^2$的加速度加速到原速率$v_0$继续行驶。已知弯道的半径$R = 24\ m$。弯道圆弧长度$s = 60\ m$,转弯时路面对轮胎的径向最大静摩擦力为车重的 0.6 倍,重力加速度大小$g$取$10\ m/s^2$,求
(1)汽车开始刹车时距$B$的距离;
(2)汽车从刹车开始至恢复到原速率所用的时间。
(1)汽车开始刹车时距$B$的距离;
(2)汽车从刹车开始至恢复到原速率所用的时间。

答案:
13.匀变速直线运动+圆周运动 【2025课标新变化:在教材编写建议中新增“作业设计要联系实际,注重情境创设”】
(1) 汽车以不发生侧滑的最大速率通过圆弧弯道,则此时最大静摩擦力提供向心力,已知弯道的半径$R = 24m$,转弯时路面对轮胎的径向最大静摩擦力为车重的0.6倍,则在BC段根据牛顿第二定律有$0.6mg = m\frac{v^{2}}{R}$,解得汽车通过圆弧弯道的速率为$v = 12m/s$
对AB段刹车过程,根据速度位移公式有$v^{2} - v^{2}_{0} = - 2a_{1}x$,解得开始刹车时汽车距B的距离为$x = 32m$
(2) 在AB段,汽车从刹车开始做匀减速直线运动,根据速度时间公式有$v = v_{0} - a_{1}t_{1}$,解得汽车从刹车开始至B所用时间$t_{1} = 2s$
在BC段,汽车做匀速圆周运动,已知圆弧弯道长度$s = 60m$,根据圆周运动线速度的定义式可知$v = \frac{s}{t_{2}}$,解得汽车通过圆弧弯道的时间$t_{2} = 5s$
在CD段,汽车做匀加速直线运动加速到原速率,根据速度时间公式可知$v_{0} = v + a_{2}t_{3}$,解得汽车从C点至恢复到原速率的时间$t_{3} = 4s$
故汽车从刹车开始至恢复到原速率所用时间为$t = t_{1} + t_{2} + t_{3} = 11s$
(1) 汽车以不发生侧滑的最大速率通过圆弧弯道,则此时最大静摩擦力提供向心力,已知弯道的半径$R = 24m$,转弯时路面对轮胎的径向最大静摩擦力为车重的0.6倍,则在BC段根据牛顿第二定律有$0.6mg = m\frac{v^{2}}{R}$,解得汽车通过圆弧弯道的速率为$v = 12m/s$
对AB段刹车过程,根据速度位移公式有$v^{2} - v^{2}_{0} = - 2a_{1}x$,解得开始刹车时汽车距B的距离为$x = 32m$
(2) 在AB段,汽车从刹车开始做匀减速直线运动,根据速度时间公式有$v = v_{0} - a_{1}t_{1}$,解得汽车从刹车开始至B所用时间$t_{1} = 2s$
在BC段,汽车做匀速圆周运动,已知圆弧弯道长度$s = 60m$,根据圆周运动线速度的定义式可知$v = \frac{s}{t_{2}}$,解得汽车通过圆弧弯道的时间$t_{2} = 5s$
在CD段,汽车做匀加速直线运动加速到原速率,根据速度时间公式可知$v_{0} = v + a_{2}t_{3}$,解得汽车从C点至恢复到原速率的时间$t_{3} = 4s$
故汽车从刹车开始至恢复到原速率所用时间为$t = t_{1} + t_{2} + t_{3} = 11s$
查看更多完整答案,请扫码查看


