第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
四、按要求涂色。(每题2分,共8分)
1. 指针一定停在红色区域。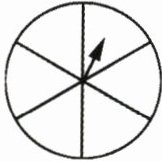
2. 指针不可能停在红色区域。
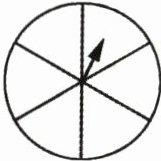
3. 指针停在蓝色区域的可能性最大。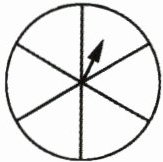
4. 指针停在绿色区域 的可能性最小。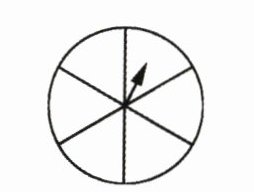
1. 指针一定停在红色区域。

2. 指针不可能停在红色区域。

3. 指针停在蓝色区域的可能性最大。

4. 指针停在绿色区域 的可能性最小。

答案:
1. 把整个圆都涂成红色。
2. 不涂红色(涂其他颜色)。
3. 涂蓝色的区域最多(比如涂4块蓝色,其他颜色涂较少块数)。
4. 涂绿色的区域最少(比如涂1块绿色,其他颜色涂较多块数)。
2. 不涂红色(涂其他颜色)。
3. 涂蓝色的区域最多(比如涂4块蓝色,其他颜色涂较少块数)。
4. 涂绿色的区域最少(比如涂1块绿色,其他颜色涂较多块数)。
五、评价与反思。(共7分)
国庆节期间,某购物广场举办有奖销售活动,顾客购满100元即可参加摸奖活动。下面两个箱子中各有6个大小相同的乒乓球,分别写着数字1到6。摸奖公告如下。
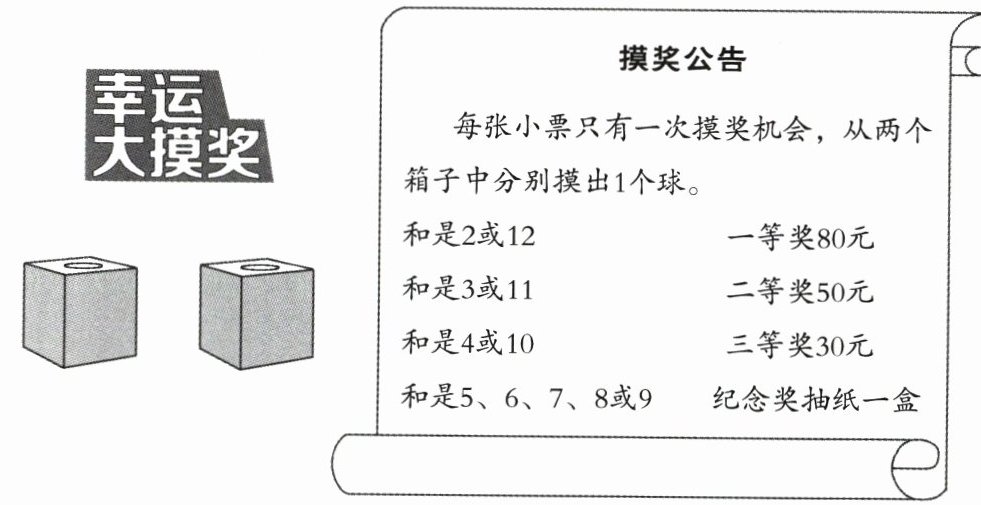
1. 李阿姨正在摸奖,请你猜一猜她最有可能获得什么奖。(3分)
2. 强强说:“这次摸到一等奖的可能性比摸到二等奖的可能性大。”你认为他说的对吗?为什么?(4分)
国庆节期间,某购物广场举办有奖销售活动,顾客购满100元即可参加摸奖活动。下面两个箱子中各有6个大小相同的乒乓球,分别写着数字1到6。摸奖公告如下。

1. 李阿姨正在摸奖,请你猜一猜她最有可能获得什么奖。(3分)
2. 强强说:“这次摸到一等奖的可能性比摸到二等奖的可能性大。”你认为他说的对吗?为什么?(4分)
答案:
1. 解:两个箱子各摸一个球,出现的和的情况有:
$1 + 1 = 2$,$1 + 2 = 3$,$1 + 3 = 4$,$1 + 4 = 5$,$1 + 5 = 6$,$1 + 6 = 7$,
$2 + 1 = 3$,$2 + 2 = 4$,$2 + 3 = 5$,$2 + 4 = 6$,$2 + 5 = 7$,$2 + 6 = 8$,
$3 + 1 = 4$,$3 + 2 = 5$,$3 + 3 = 6$,$3 + 4 = 7$,$3 + 5 = 8$,$3 + 6 = 9$,
$4 + 1 = 5$,$4 + 2 = 6$,$4 + 3 = 7$,$4 + 4 = 8$,$4 + 5 = 9$,$4 + 6 = 10$,
$5 + 1 = 6$,$5 + 2 = 7$,$5 + 3 = 8$,$5 + 4 = 9$,$5 + 5 = 10$,$5 + 6 = 11$,
$6 + 1 = 7$,$6 + 2 = 8$,$6 + 3 = 9$,$6 + 4 = 10$,$6 + 5 = 11$,$6 + 6 = 12$。
共$36$种情况。
和是$2$或$12$的情况有$2$种;和是$3$或$11$的情况有$4$种;和是$4$或$10$的情况有$6$种;和是$5$、$6$、$7$、$8$或$9$的情况有$24$种。
因为$24\gt6\gt4\gt2$,所以她最有可能获得纪念奖。
2. 解:摸到一等奖(和是$2$或$12$)的情况有$2$种,摸到二等奖(和是$3$或$11$)的情况有$4$种。
因为$2\lt4$,所以摸到一等奖的可能性比摸到二等奖的可能性小,强强说的不对。
$1 + 1 = 2$,$1 + 2 = 3$,$1 + 3 = 4$,$1 + 4 = 5$,$1 + 5 = 6$,$1 + 6 = 7$,
$2 + 1 = 3$,$2 + 2 = 4$,$2 + 3 = 5$,$2 + 4 = 6$,$2 + 5 = 7$,$2 + 6 = 8$,
$3 + 1 = 4$,$3 + 2 = 5$,$3 + 3 = 6$,$3 + 4 = 7$,$3 + 5 = 8$,$3 + 6 = 9$,
$4 + 1 = 5$,$4 + 2 = 6$,$4 + 3 = 7$,$4 + 4 = 8$,$4 + 5 = 9$,$4 + 6 = 10$,
$5 + 1 = 6$,$5 + 2 = 7$,$5 + 3 = 8$,$5 + 4 = 9$,$5 + 5 = 10$,$5 + 6 = 11$,
$6 + 1 = 7$,$6 + 2 = 8$,$6 + 3 = 9$,$6 + 4 = 10$,$6 + 5 = 11$,$6 + 6 = 12$。
共$36$种情况。
和是$2$或$12$的情况有$2$种;和是$3$或$11$的情况有$4$种;和是$4$或$10$的情况有$6$种;和是$5$、$6$、$7$、$8$或$9$的情况有$24$种。
因为$24\gt6\gt4\gt2$,所以她最有可能获得纪念奖。
2. 解:摸到一等奖(和是$2$或$12$)的情况有$2$种,摸到二等奖(和是$3$或$11$)的情况有$4$种。
因为$2\lt4$,所以摸到一等奖的可能性比摸到二等奖的可能性小,强强说的不对。
查看更多完整答案,请扫码查看


