一、解方程。
$ \frac{3}{4}x + \frac{1}{2}x = \frac{9}{4} $
$ x - \frac{3}{4}x = 15 $
$ 6x + 5x = \frac{22}{23} $
$ \left( \frac{3}{8} - \frac{1}{4} \right)x = \frac{3}{8} $
$ \frac{3}{4}x + \frac{1}{2}x = \frac{9}{4} $
$ x - \frac{3}{4}x = 15 $
$ 6x + 5x = \frac{22}{23} $
$ \left( \frac{3}{8} - \frac{1}{4} \right)x = \frac{3}{8} $
答案:
$x=\frac{9}{5}$ $x=60$ $x=\frac{2}{23}$ $x=3$
二、计算下面各题。
$ 6 - \left( \frac{1}{7} + \frac{1}{4} \right) $
$ \left( \frac{1}{4} + \frac{7}{8} \right) ÷ \frac{6}{7} $
$ \left( 1 - \frac{1}{4} × \frac{8}{9} \right) ÷ \frac{7}{9} $
$ 12 ÷ \left[ \left( \frac{7}{9} - \frac{2}{3} \right) × \frac{9}{10} \right] $
$ 6 - \left( \frac{1}{7} + \frac{1}{4} \right) $
$ \left( \frac{1}{4} + \frac{7}{8} \right) ÷ \frac{6}{7} $
$ \left( 1 - \frac{1}{4} × \frac{8}{9} \right) ÷ \frac{7}{9} $
$ 12 ÷ \left[ \left( \frac{7}{9} - \frac{2}{3} \right) × \frac{9}{10} \right] $
答案:
$5\frac{17}{28}$ $\frac{21}{16}$ 1 120
三、求下面图形的表面积和体积。
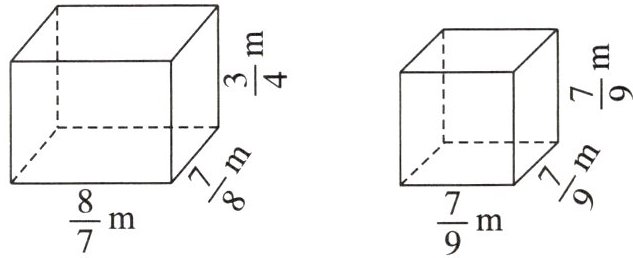

答案:
$(\frac{8}{7}×\frac{7}{8}+\frac{8}{7}×\frac{3}{4}+\frac{7}{8}×\frac{3}{4})×2=\frac{563}{112}$(平方米)
$\frac{8}{7}×\frac{7}{8}×\frac{3}{4}=\frac{3}{4}$(立方米)
$\frac{7}{9}×\frac{7}{9}×6=\frac{98}{27}$(平方米)
$\frac{7}{9}×\frac{7}{9}×\frac{7}{9}=\frac{343}{729}$(立方米)
$\frac{8}{7}×\frac{7}{8}×\frac{3}{4}=\frac{3}{4}$(立方米)
$\frac{7}{9}×\frac{7}{9}×6=\frac{98}{27}$(平方米)
$\frac{7}{9}×\frac{7}{9}×\frac{7}{9}=\frac{343}{729}$(立方米)
四、农场发起“节约用电”活动。农场 4 月份用电 330 千瓦时,5 月份比 4 月份节约 $$ \frac{2}{11} $$。5 月份用电多少千瓦时?
答案:
$330×(1-\frac{2}{11})=270$(千瓦时)
五、两台小麦收割机,第一台 $$ \frac{3}{4} $$ 小时收割小麦 3 公顷,第二台每小时收割小麦 3 公顷。两台收割机同时收割 91 公顷小麦,需要多少小时?
答案:
$91÷(3÷\frac{3}{4}+3)=13$(时)
六、小文把$ \left( a + \frac{5}{11} \right) × 6 错当成 a + \frac{5}{11} × 6 $进行计算,这样算出的结果与正确结果相差多少?
答案:
$(a+\frac{5}{11})×6-(a+\frac{5}{11}×6)=6a-a=5a$

答案:
1. 计算$\frac{2}{3}×\frac{7}{8}$:
根据分数乘法法则$\frac{a}{b}×\frac{c}{d}=\frac{ac}{bd}$($b\neq0$,$d\neq0$),则$\frac{2}{3}×\frac{7}{8}=\frac{2×7}{3×8}=\frac{14}{24}=\frac{7}{12}$。
2. 计算$\frac{3}{4}+\frac{1}{2}$:
先通分,$\frac{1}{2}=\frac{1×2}{2×2}=\frac{2}{4}$,再根据同分母分数加法法则$\frac{a}{c}+\frac{b}{c}=\frac{a + b}{c}$($c\neq0$),则$\frac{3}{4}+\frac{1}{2}=\frac{3}{4}+\frac{2}{4}=\frac{3 + 2}{4}=\frac{5}{4}$。
3. 计算$\frac{5}{9}-\frac{1}{5}$:
先通分,$\frac{5}{9}=\frac{5×5}{9×5}=\frac{25}{45}$,$\frac{1}{5}=\frac{1×9}{5×9}=\frac{9}{45}$,再根据同分母分数减法法则$\frac{a}{c}-\frac{b}{c}=\frac{a - b}{c}$($c\neq0$),则$\frac{5}{9}-\frac{1}{5}=\frac{25}{45}-\frac{9}{45}=\frac{25 - 9}{45}=\frac{16}{45}$。
4. 计算$\frac{2}{5}÷\frac{4}{7}$:
根据分数除法法则$\frac{a}{b}÷\frac{c}{d}=\frac{a}{b}×\frac{d}{c}$($b\neq0$,$c\neq0$,$d\neq0$),则$\frac{2}{5}÷\frac{4}{7}=\frac{2}{5}×\frac{7}{4}=\frac{2×7}{5×4}=\frac{14}{20}=\frac{7}{10}$。
5. 计算$1-\frac{3}{8}$:
把$1$看成$\frac{8}{8}$,再根据同分母分数减法法则$\frac{a}{c}-\frac{b}{c}=\frac{a - b}{c}$($c\neq0$),则$1-\frac{3}{8}=\frac{8}{8}-\frac{3}{8}=\frac{8 - 3}{8}=\frac{5}{8}$。
6. 计算$42÷\frac{7}{13}$:
根据分数除法法则$a÷\frac{b}{c}=a×\frac{c}{b}$($a = 42$,$b = 7$,$c = 13$),则$42÷\frac{7}{13}=42×\frac{13}{7}$,$42÷7 = 6$,所以$42×\frac{13}{7}=6×13 = 78$。
7. 计算$\frac{3}{5}×25$:
根据分数乘法法则$\frac{a}{b}× c=\frac{ac}{b}$($b\neq0$),则$\frac{3}{5}×25=\frac{3×25}{5}=3×5 = 15$。
8. 计算$\frac{5}{6}+\frac{2}{3}$:
先通分,$\frac{2}{3}=\frac{2×2}{3×2}=\frac{4}{6}$,再根据同分母分数加法法则$\frac{a}{c}+\frac{b}{c}=\frac{a + b}{c}$($c\neq0$),则$\frac{5}{6}+\frac{2}{3}=\frac{5}{6}+\frac{4}{6}=\frac{5 + 4}{6}=\frac{9}{6}=\frac{3}{2}$。
综上,答案依次为:$\frac{7}{12}$;$\frac{5}{4}$;$\frac{16}{45}$;$\frac{7}{10}$;$\frac{5}{8}$;$78$;$15$;$\frac{3}{2}$。
根据分数乘法法则$\frac{a}{b}×\frac{c}{d}=\frac{ac}{bd}$($b\neq0$,$d\neq0$),则$\frac{2}{3}×\frac{7}{8}=\frac{2×7}{3×8}=\frac{14}{24}=\frac{7}{12}$。
2. 计算$\frac{3}{4}+\frac{1}{2}$:
先通分,$\frac{1}{2}=\frac{1×2}{2×2}=\frac{2}{4}$,再根据同分母分数加法法则$\frac{a}{c}+\frac{b}{c}=\frac{a + b}{c}$($c\neq0$),则$\frac{3}{4}+\frac{1}{2}=\frac{3}{4}+\frac{2}{4}=\frac{3 + 2}{4}=\frac{5}{4}$。
3. 计算$\frac{5}{9}-\frac{1}{5}$:
先通分,$\frac{5}{9}=\frac{5×5}{9×5}=\frac{25}{45}$,$\frac{1}{5}=\frac{1×9}{5×9}=\frac{9}{45}$,再根据同分母分数减法法则$\frac{a}{c}-\frac{b}{c}=\frac{a - b}{c}$($c\neq0$),则$\frac{5}{9}-\frac{1}{5}=\frac{25}{45}-\frac{9}{45}=\frac{25 - 9}{45}=\frac{16}{45}$。
4. 计算$\frac{2}{5}÷\frac{4}{7}$:
根据分数除法法则$\frac{a}{b}÷\frac{c}{d}=\frac{a}{b}×\frac{d}{c}$($b\neq0$,$c\neq0$,$d\neq0$),则$\frac{2}{5}÷\frac{4}{7}=\frac{2}{5}×\frac{7}{4}=\frac{2×7}{5×4}=\frac{14}{20}=\frac{7}{10}$。
5. 计算$1-\frac{3}{8}$:
把$1$看成$\frac{8}{8}$,再根据同分母分数减法法则$\frac{a}{c}-\frac{b}{c}=\frac{a - b}{c}$($c\neq0$),则$1-\frac{3}{8}=\frac{8}{8}-\frac{3}{8}=\frac{8 - 3}{8}=\frac{5}{8}$。
6. 计算$42÷\frac{7}{13}$:
根据分数除法法则$a÷\frac{b}{c}=a×\frac{c}{b}$($a = 42$,$b = 7$,$c = 13$),则$42÷\frac{7}{13}=42×\frac{13}{7}$,$42÷7 = 6$,所以$42×\frac{13}{7}=6×13 = 78$。
7. 计算$\frac{3}{5}×25$:
根据分数乘法法则$\frac{a}{b}× c=\frac{ac}{b}$($b\neq0$),则$\frac{3}{5}×25=\frac{3×25}{5}=3×5 = 15$。
8. 计算$\frac{5}{6}+\frac{2}{3}$:
先通分,$\frac{2}{3}=\frac{2×2}{3×2}=\frac{4}{6}$,再根据同分母分数加法法则$\frac{a}{c}+\frac{b}{c}=\frac{a + b}{c}$($c\neq0$),则$\frac{5}{6}+\frac{2}{3}=\frac{5}{6}+\frac{4}{6}=\frac{5 + 4}{6}=\frac{9}{6}=\frac{3}{2}$。
综上,答案依次为:$\frac{7}{12}$;$\frac{5}{4}$;$\frac{16}{45}$;$\frac{7}{10}$;$\frac{5}{8}$;$78$;$15$;$\frac{3}{2}$。
查看更多完整答案,请扫码查看


