(1)几个数共有的因数,叫作这几个数的
公因数
,其中最小的一个是1
,最大的是它们的最大公因数
。
答案:
公因数
1
最大公因数
有限
1
最大公因数
有限
(2)一个数的因数的个数是
有限
的。
答案:
有限
(3)6 的因数有(
1, 2, 3, 6
),8 的因数有(1, 2, 4, 8
),6 和 8 的公因数是(1, 2
),6 和8 的最大公因数是(2
)。
答案:
6 的因数有( 1, 2, 3, 6 ),
8 的因数有( 1, 2, 4, 8 ),
6 和 8 的公因数是( 1, 2 ),
6 和 8 的最大公因数是( 2 )。
8 的因数有( 1, 2, 4, 8 ),
6 和 8 的公因数是( 1, 2 ),
6 和 8 的最大公因数是( 2 )。
(4)填一填。

20 和 30 的最大公因数是( )。

20 和 30 的最大公因数是( )。
答案:
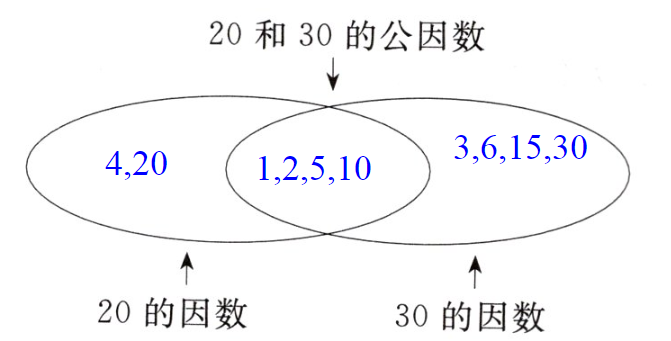 10
10
 10
10 2.写出下面各组数的最大公因数,并仔细观察每组数的特点。
5 和 11(
发现了:
5 和 11(
1
) 8 和 9(1
) 6 和 7(1
) 9 和 4(1
)发现了:
当两个数的公因数只有1时,1就是最大公因数。
答案:
1
1
1
1
当两个数的公因数只有1时,1就是最大公因数。
1
1
1
当两个数的公因数只有1时,1就是最大公因数。
3.写出下面各组数的最大公因数,并仔细观察每组数的特点。
3 和 15(
发现了:
3 和 15(
3
) 6 和 18(6
) 12 和 36(12
) 8 和 24(8
)发现了:
最大公因数是前面一个数。
答案:
3
6
12
8
最大公因数是前面一个数。
6
12
8
最大公因数是前面一个数。
4.判断。(正确的在括号内画“√”,错误的画“×”。)
(1)如果两个数是质数,它们就没有公因数和最大公因数。(
(2)两个合数,它们一定有两个以上的公因数。(
(3)1 是所有非 0 自然数的公因数。(
(4)相邻的两个非零自然数的最大公因数是 1。(
(1)如果两个数是质数,它们就没有公因数和最大公因数。(
×
)(2)两个合数,它们一定有两个以上的公因数。(
×
)(3)1 是所有非 0 自然数的公因数。(
√
)(4)相邻的两个非零自然数的最大公因数是 1。(
√
)
答案:
×
×
√
√
×
√
√
5.有一面长方形墙,长 40dm,高 24dm。要用边长是整分米数的正方形瓷砖把这面墙贴满(瓷砖不能切割),可以选择边长是多少分米的瓷砖?边长最长是多少分米?
(1)要使所有的正方瓷砖都是整块的,瓷砖的边长必须是 40 和 24 的
(2)我是这样解决的:40的因数:1,2,4,5,8,10,20,40
24的因数:1,2,3,4,6,8,12,24
40和24的公因数:1,2,4,8
可以选择边长是1dm,2dm,4dm,8dm的瓷砖,边长最长是8dm。
(3)右面就是这面墙,请用符合要求的、最大的正方形瓷砖画一画、验一验。

(1)要使所有的正方瓷砖都是整块的,瓷砖的边长必须是 40 和 24 的
公因数
。(2)我是这样解决的:40的因数:1,2,4,5,8,10,20,40
24的因数:1,2,3,4,6,8,12,24
40和24的公因数:1,2,4,8
可以选择边长是1dm,2dm,4dm,8dm的瓷砖,边长最长是8dm。
(3)右面就是这面墙,请用符合要求的、最大的正方形瓷砖画一画、验一验。

(画图略,需在长方形内画出边长为8dm的正方形瓷砖,每行5块,共3行,恰好贴满)
答案:
(1)公因数
(2)40的因数:1,2,4,5,8,10,20,40
24的因数:1,2,3,4,6,8,12,24
40和24的公因数:1,2,4,8
可以选择边长是1dm,2dm,4dm,8dm的瓷砖,边长最长是8dm。
(3)(画图略,需在长方形内画出边长为8dm的正方形瓷砖,每行5块,共3行,恰好贴满)
(1)公因数
(2)40的因数:1,2,4,5,8,10,20,40
24的因数:1,2,3,4,6,8,12,24
40和24的公因数:1,2,4,8
可以选择边长是1dm,2dm,4dm,8dm的瓷砖,边长最长是8dm。
(3)(画图略,需在长方形内画出边长为8dm的正方形瓷砖,每行5块,共3行,恰好贴满)
查看更多完整答案,请扫码查看


