《2025年学习之友五年级数学上册北师大版》

1.填一填。

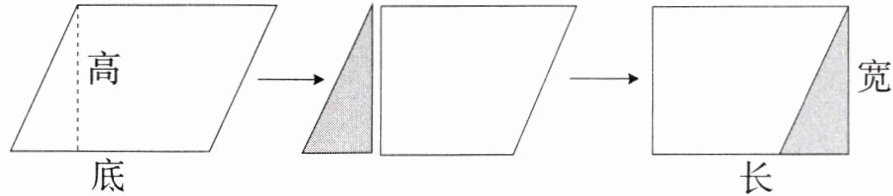
长方形的长= 平行四边形的底
长方形的宽= 平行四边形的高
长方形的面积= 长×宽
平行四边形的面积= 底×高

答案： 平行四边形的底；平行四边形的高；长×宽；底×高

2.请你再画一画、说一说三角形或梯形的面积公式推导过程吧!______

答案： 三角形面积公式推导：
1. 画图：画两个完全相同的三角形，将它们拼成一个平行四边形。
2. 推导：平行四边形面积=底×高，三角形面积=平行四边形面积÷2，故三角形面积=底×高÷2（公式：$S=\frac{1}{2}ah$，$a$为底，$h$为高）。
梯形面积公式推导：
1. 画图：画两个完全相同的梯形，将它们拼成一个平行四边形。
2. 推导：平行四边形的底=梯形上底+下底，高=梯形的高，平行四边形面积=（上底+下底）×高，梯形面积=平行四边形面积÷2，故梯形面积=（上底+下底）×高÷2（公式：$S=\frac{1}{2}(a+b)h$，$a$为上底，$b$为下底，$h$为高）。

1.梯形的面积公式能否计算平行四边形的面积呢?请你画图并说明你的想法。______

答案： 梯形的面积公式能计算平行四边形的面积。
画图：（此处可画一个平行四边形，标注上底$a$、下底$b$、高$h$，其中$a = b$）
说明：梯形面积公式为$S=\frac{(上底 + 下底)×高}{2}$。平行四边形的两组对边分别平行且相等，即上底$a$等于下底$b$。代入梯形面积公式得$S=\frac{(a + a)× h}{2}=\frac{2a× h}{2}=a× h$，此即为平行四边形的面积公式。因此，梯形面积公式可计算平行四边形的面积。

2.梯形的面积公式能否计算三角形的面积呢?请你画图并说明你的想法。______

答案： 能。当梯形的上底长度逐渐缩短至0时，梯形转化为三角形。此时梯形面积公式为：（上底+下底）×高÷2 =（0+底）×高÷2 = 底×高÷2，即三角形面积公式。