(1)等底等高的平行四边形的面积
相等
。
答案:
相等
(2)一块平行四边形的菜地,面积是48平方米,高是4米,底是(
12
)米。
答案:
12
(3)一块平行四边形草坪,它的高是8米,底是高的2倍,它的面积是(
128
)平方米。
答案:
128
2.按要求填表。
| 平行四边形 | 底/cm | 高/cm | 面积$/cm^2 $|
| | 7 | | 147 |
| | 3.6 | 3 | |
| | 4.2 | | 21 |

| 平行四边形 | 底/cm | 高/cm | 面积$/cm^2 $|
| | 7 | | 147 |
| | 3.6 | 3 | |
| | 4.2 | | 21 |

答案:
21;10.8;5
(1)用木条钉成的长方形拉成一个平行四边形,它的面积
A.不变
B.比原来大
C.比原来小
C
。A.不变
B.比原来大
C.比原来小
答案:
C
(2)一个平行四边形的底扩大到原来的2倍,高不变,则面积(
A.不变
B.扩大到原来的2倍
C.扩大到原来的4倍
B
)。A.不变
B.扩大到原来的2倍
C.扩大到原来的4倍
答案:
B
4.如图,正方形的周长是32厘米,求阴影部分平行四边形的面积。


答案:
32÷4=8(厘米)
8×8=64(平方厘米)
答:阴影部分平行四边形的面积是64平方厘米。
5.观察下图,甲、乙、丙三个平行四边形的面积有什么变化规律。
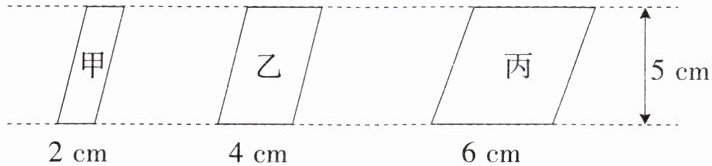
(1)请分别计算出甲、乙、丙三个平行四边形的面积。
(2)请提出有深度的数学问题或猜想。

(1)请分别计算出甲、乙、丙三个平行四边形的面积。
(2)请提出有深度的数学问题或猜想。
答案:
(1)
甲平行四边形面积:$S = 底×高=2×5 = 10$($cm^{2}$)
乙平行四边形面积:$S = 底×高=4×5 = 20$($cm^{2}$)
丙平行四边形面积:$S = 底×高=6×5 = 30$($cm^{2}$)
(2)
猜想:等高的平行四边形,面积随底边长的增大而增大,且面积与底边长成正比关系。
(1)
甲平行四边形面积:$S = 底×高=2×5 = 10$($cm^{2}$)
乙平行四边形面积:$S = 底×高=4×5 = 20$($cm^{2}$)
丙平行四边形面积:$S = 底×高=6×5 = 30$($cm^{2}$)
(2)
猜想:等高的平行四边形,面积随底边长的增大而增大,且面积与底边长成正比关系。
查看更多完整答案,请扫码查看


