《2025年新课标学习方法指导丛书三年级数学上册人教版》

1. 列竖式计算。
206×3＝ 206
× 3
-----
618 950×4＝ 950
× 4
-----
3800 507×9＝ 507
× 9
-----
4563 780×6＝ 780
× 6
-----
4680

答案： ```
206
× 3
-----
618
950
× 4
-----
3800
507
× 9
-----
4563
780
× 6
-----
4680
```

(1)与320×5的积不相等的是(A)。
A.300＋20×5
B.300×5＋20×5
C.40×5×8

答案： 解析：本题可根据乘法分配律以及乘法结合律分别对选项进行分析，再与$320×5$的积进行比较。
选项A：
根据四则运算顺序，先计算乘法再计算加法，$300 + 20×5=300 + 100 = 400$。
而$320×5 = 1600$，$400\neq1600$，所以该选项与$320×5$的积不相等。
选项B：
把$320$拆分成$300 + 20$，根据乘法分配律$(a + b)×c = a×c + b×c$，可得$(300 + 20)×5 = 300×5 + 20×5$，$300×5 + 20×5=1500 + 100 = 1600$，$1600$与$320×5$的积相等。
选项C：
把$320$拆分成$40×8$，根据乘法结合律$(a×b)×c = a×(b×c)$，可得$40×8×5 = 40×(8×5)=40×40 = 1600$，$1600$与$320×5$的积相等。
答案：A

(2)王老师要给三(1)班的学生买一些单价8元的笔记本作为奖品,奖品数量在30本和40本之间,奖品总价钱可能是(C)。
A.200元
B.336元
C.288元
D.283元

答案： 解析：本题考查单价、数量和总价之间的关系。
根据总价=单价×数量，
笔记本的单价是8元，数量在30本和40本之间，可得：
最少总价：$8 × 30 = 240$（元），
最多总价：$8 × 40 = 320$（元），
所以奖品的总价钱在240元和320元之间。
接下来，我们来看选项：
A. 200元：不在240元和320元之间，所以A选项错误。
B. 336元：不在240元和320元之间，所以B选项错误。
C. 288元：在240元和320元之间，符合条件，所以C选项正确。
D. 283元：虽然也在240元和320元之间，但是我们需要找到符合条件的所有选项，并确定最可能的答案。由于题目问的是“可能”的总价钱，且C选项已经是一个符合条件的答案，但我们需要继续判断D是否也符合条件，经判断D虽然符合条件但不是唯一答案，我们需要选出所有符合条件的，而题目是单选，通过比较C选项288是8的倍数，
$288{÷} 8=36$，在30到40之间，符合题目条件，而283不是8的倍数，所以相对C选项，D不是正确答案。
答案：C

(3)算式(A)的积可能是图中点P表示的数。算式(C)的积可能是图中点Q表示的数。
A.42×7
B.3×88
C.51×8
D.49×9

答案： 解析：本题考查两位数乘一位数的估算。
图中点$P$表示的数在$260\sim 280$之间，接近$280$；点$Q$表示的数在$400\sim 420$之间，接近$420$。
A选项：$42×7\approx40×7 = 280$，符合点$P$的范围。
B选项：$3×88\approx3×90 = 270$，不在点$P$和点$Q$的范围内。
C选项：$51×8\approx50×8 = 400$，符合点$Q$的范围。
D选项：$49×9\approx50×9 = 450$，不在点$P$和点$Q$的范围内。
答案：A；C。

(4)计算三位数乘一位数,下面说法正确的是(C)。
A.三位数的中间没有0,积的中间也没有0
B.三位数的中间有0,积的中间一定也有0
C.三位数的末尾有0,积的末尾一定有0
D.三位数的末尾没有0,积的末尾也没有0

答案： 解析：
本题考查三位数乘一位数的运算规律。
A选项：三位数的中间没有0，并不意味着积的中间也没有0。例如，123×4=492，积的中间没有0，但如果考虑125×8=1000，积的中间有0，所以A选项错误。
B选项：三位数的中间有0，并不意味着积的中间一定也有0。例如，105×3=315，积的中间没有0，所以B选项错误。
C选项：三位数的末尾有0，意味着这个数是10的倍数，因此它与任何数的乘积都将是10的倍数，即积的末尾一定有0。所以C选项正确。
D选项：三位数的末尾没有0，并不意味着积的末尾也没有0。例如，125×8=1000，积的末尾有0，所以D选项错误。
答案：(C)。

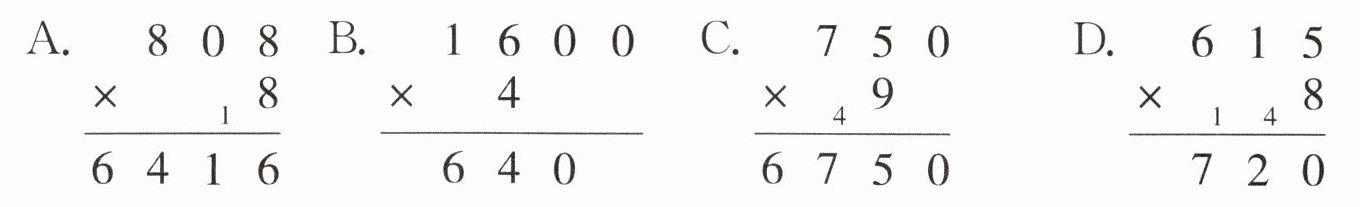
(5)下面4个竖式中,计算正确的是(C)。

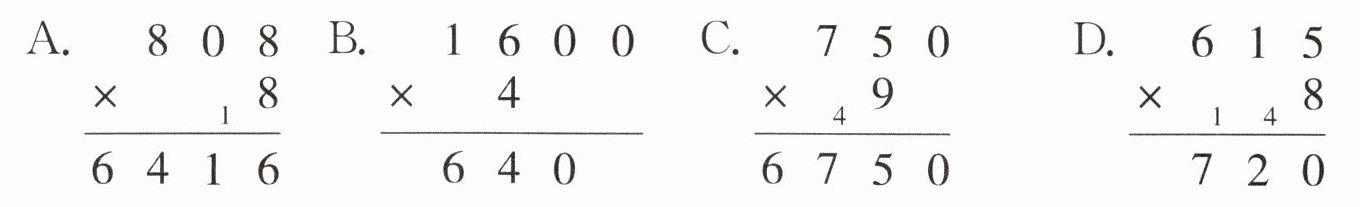
答案： C