第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1 填一填。
(1)一瓶$\frac{4}{5}\ L$的饮料。小滨喝了3瓶,求小滨喝了多少升,列式为$\frac{4}{5}×3$,这个算式表示(
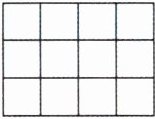
(2)如图,整个长方形的面积是$\frac{3}{4}\ dm^2$,涂色部分的面积是(
(1)一瓶$\frac{4}{5}\ L$的饮料。小滨喝了3瓶,求小滨喝了多少升,列式为$\frac{4}{5}×3$,这个算式表示(
$\frac{4}{5}$的3倍是多少
);小西喝了$\frac{2}{3}$瓶,求小西喝了多少升,列式为$\frac{4}{5}×\frac{2}{3}$,这个算式表示($\frac{4}{5}$的$\frac{2}{3}$是多少
)。(2)如图,整个长方形的面积是$\frac{3}{4}\ dm^2$,涂色部分的面积是(
$\frac{5}{16}$
)$dm^2$。
答案:
(1)$\frac{4}{5}$的3倍是多少 $\frac{4}{5}$的$\frac{2}{3}$是多少
(2)$\frac{5}{16}$
(1)$\frac{4}{5}$的3倍是多少 $\frac{4}{5}$的$\frac{2}{3}$是多少
(2)$\frac{5}{16}$
2 数学课上,三名同学在图中用涂色的方式表达了自己对$6×\frac{2}{3}$的理解,其中正确的(

A.只有小西
B.只有小西、小宸
C.只有小宸、小滨
D.有小西、小宸、小滨
B
)。
A.只有小西
B.只有小西、小宸
C.只有小宸、小滨
D.有小西、小宸、小滨
答案:
B
3 直接写出得数。
$\frac{4}{7}×\frac{3}{8}=$(
$\frac{5}{28}×7=$(
$12×\frac{3}{5}=$(
$\frac{13}{30}×\frac{30}{26}=$(
$\frac{4}{7}×\frac{3}{8}=$(
$\frac{3}{14}$
)$\frac{5}{28}×7=$(
$\frac{5}{4}$
)$12×\frac{3}{5}=$(
$\frac{36}{5}$
)$\frac{13}{30}×\frac{30}{26}=$(
$\frac{1}{2}$
)
答案:
$\frac{3}{14}$ $\frac{5}{4}$ $\frac{36}{5}$ $\frac{1}{2}$
4 小滨每天的作息情况如下:①休息时间占$\frac{5}{12}$;②书法练习时间占$\frac{1}{36}$;③体育锻炼时间占$\frac{1}{16}$;④课外阅读时间占$\frac{1}{24}$……请从以上信息中选择1~3条,再根据你选择的信息提出一个数学问题并解答。
信息:(
问题:(
解答:
信息:(
①
)(填序号)问题:(
小滨每天休息多长时间?
)解答:
答案:
答案不唯一,合理即可。如:① 小滨每天休息多长时间?$24×\frac{5}{12}=10$(时)答:小滨每天休息10小时。
5〔大单元关联〕学习分数乘分数计算时,我们运用画图、举例的策略推理得到“分数与分数相乘,用分子相乘的积作分子,分母相乘的积作分母”。
小滨:整数乘整数,计数单位与计数单位相乘作积的计数单位,每个乘数的计数单位个数相乘,产生新的计数单位个数。计数单位和计数单位的个数都确定了,结果也就确定了。
小西:我觉得可以这样解释:$30×500= (10×3)×(100×5)= (10×100)×(3×5)= 1000×15= 15000$。
小宸:我觉得小数乘法和整数乘法的运算道理是一样的,也可以像小西那样计算。例如:$0.3×0.07= (3×0.1)×(7×0.01)= (3×7)×(0.1×0.01)= 21×0.001= 0.021$。
小余:我觉得分数乘法与整数、小数乘法的运算道理是一致的。你同意小余的观点吗?如果同意,请以$\frac{2}{7}×\frac{5}{9}$为例写出计算过程。
小滨:整数乘整数,计数单位与计数单位相乘作积的计数单位,每个乘数的计数单位个数相乘,产生新的计数单位个数。计数单位和计数单位的个数都确定了,结果也就确定了。
小西:我觉得可以这样解释:$30×500= (10×3)×(100×5)= (10×100)×(3×5)= 1000×15= 15000$。
小宸:我觉得小数乘法和整数乘法的运算道理是一样的,也可以像小西那样计算。例如:$0.3×0.07= (3×0.1)×(7×0.01)= (3×7)×(0.1×0.01)= 21×0.001= 0.021$。
小余:我觉得分数乘法与整数、小数乘法的运算道理是一致的。你同意小余的观点吗?如果同意,请以$\frac{2}{7}×\frac{5}{9}$为例写出计算过程。
答案:
我同意小余的观点。计算过程如下:$\frac{2}{7}×\frac{5}{9}=(\frac{1}{7}×2)×(\frac{1}{9}×5)=(\frac{1}{7}×\frac{1}{9})×(2×5)=\frac{1}{63}×10=\frac{10}{63}$
查看更多完整答案,请扫码查看


