《2025年豫新锐暑假作业中原农民出版社八年级数学湘教版》

9. 某通信公司推出①②两种通信收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的收费 $ y $(元)与通信时间 $ x $($ \mathrm{min} $)之间的函数关系图象如图所示。

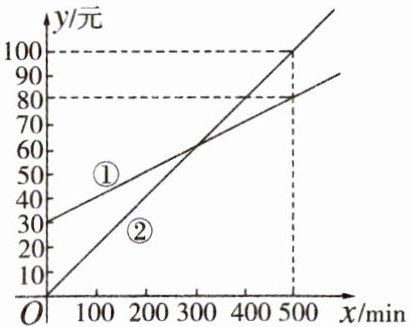
(1) 有月租费的收费方式是①(填①或②),月租费是30元；
(2) 分别求出①②两种收费方式中 $ y $ 与自变量 $ x $ 之间的函数关系式；
(3) 请你根据用户通信时间的多少,给出经济实惠的选择建议。

答案：
(1)① 30
(2)设①的函数关系式为$y = k_1x + b$，由图知，当$x = 0$时，$y = 30$，即$b = 30$；当$x = 500$时，$y = 80$，代入得$80 = 500k_1 + 30$，解得$k_1=\frac{1}{10}$，所以①：$y=\frac{1}{10}x + 30$。
设②的函数关系式为$y = k_2x$，由图知，当$x = 500$时，$y = 100$，代入得$100 = 500k_2$，解得$k_2=\frac{1}{5}$，所以②：$y=\frac{1}{5}x$。
(3)令$\frac{1}{10}x + 30=\frac{1}{5}x$，解得$x = 300$。
当$0 ＜ x ＜ 300$时，选②；当$x = 300$时，①②一样；当$x＞300$时，选①。

10. 如图,$ A $,$ B $ 两个小镇在河流 $ l $ 的同侧,到河流的距离分别为 $ AC = 10 \mathrm{~km} $,$ BD = 30 \mathrm{~km} $,且 $ CD = 30 \mathrm{~km} $,现在要在河边建一自来水厂,向 $ A $,$ B $ 两镇供水,铺设水管的费用为每千米 $ 3 $ 万元,请你在河流 $ l $ 上确定自来水厂的位置 $ M $,使铺设水管的费用最节省,并求出总费用是多少。

答案： 【解析】：
先作点$A$关于河流$l$（即直线$CD$）的对称点$A'$，连接$A'B$，与$CD$交于点$M$，则点$M$就是所求的自来水厂的位置。
接下来求$A'B$的长度。
延长$BD$，与$A'C$的延长线交于点$N$。
在直角三角形$A'BN$中，$A'N = CD = 30$（$km$）（因为$A$和$A'$关于$CD$对称，所以$AC = A'C = 10$（$km$），进而$A'N = A'C + CD=10+ 20 = 30$（$km$）），$BN = BD + DN = BD + AC = 30 + 10 = 40$（$km$），且$A'B$为斜边。
根据勾股定理，有$A'B^2 = A'N^2 + BN^2 = 30^2 + 40^2 = 900 + 1600 = 2500$，
所以$A'B = \sqrt{2500} = 50$（$km$）。
因此，铺设水管的费用为$50 × 3 = 150$（万元）。
【答案】：
位置：作点$A$关于河流$l$的对称点$A'$，连接$A'B$，与$CD$交于点$M$，则$M$为自来水厂的位置；
总费用：$150$万元。