《2025年豫新锐暑假作业中原农民出版社八年级数学湘教版》

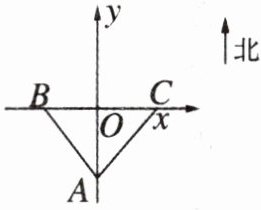
24. 某路段规定汽车的最高行驶速度不能超过 $ 60 \text{ km/h} $(即 $ \frac{50}{3} \text{ m/s} $),为了能更为详细地获知该路段的机动车行驶情况,交通管理部门选取了一段笔直的公路,在离该公路 $ 80 \text{ m} $ 处设置了一个速度监测点 $ A $,在如图的直角坐标系中,点 $ A $ 位于 $ y $ 轴上,被测速的路段 $ BC $ 在 $ x $ 轴上.已测得点 $ B $ 在点 $ A $ 的北偏西方向上,且 $ AB= 100 \text{ m} $,点 $ C $ 在点 $ A $ 的北偏东 $ 45^{\circ} $ 方向上.
(1) 求点 $ B $,$ C $ 的坐标.
(2) 若一辆汽车从点 $ B $ 行驶到点 $ C $ 共用时 $ 15 \text{ s} $,请你通过计算,判断该汽车是否超速行驶？

答案：
(1)由题意得，点$A$在$y$轴上，$AO = 80m$，$BC$在$x$轴上，$\angle CAO=45^{\circ}$。
在$\triangle ACO$中，$\angle AOC = 90^{\circ}$，$\angle CAO = 45^{\circ}$，所以$\triangle ACO$是等腰直角三角形，$CO=AO = 80m$，则点$C$的坐标为$(80,0)$。
在$Rt\triangle ABO$中，$AB = 100m$，$AO=80m$，由勾股定理得$OB=\sqrt{AB^{2}-AO^{2}}=\sqrt{100^{2}-80^{2}}=\sqrt{10000 - 6400}=\sqrt{3600}=60m$，所以点$B$的坐标为$(- 60,0)$。
(2)$BC=BO + OC=60 + 80=140m$，汽车从$B$到$C$的速度$v=\frac{BC}{t}=\frac{140}{15}=\frac{28}{3}m/s$。
因为$\frac{28}{3}\approx9.33m/s$，$\frac{50}{3}\approx16.67m/s$，且$\frac{28}{3}＜\frac{50}{3}$，所以该汽车没有超速行驶。