《2025年豫新锐暑假作业中原农民出版社八年级数学湘教版》

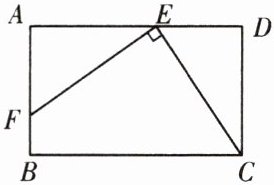
7. 如图,已知在矩形$ABCD$中,$E是AD$上的一点,$F是AB$上的一点,$EF\perp CE$,且$EF = EC$,$DE = 4\mathrm{c}\mathrm{m}$,矩形$ABCD的周长为32\mathrm{c}\mathrm{m}$,求$AE$的长。

答案： 解：
∵四边形$ABCD$是矩形，
∴$∠A = ∠D = 90^{\circ}$，$AD = BC$，$AB = DC$。
∵$EF⊥CE$，
∴$∠FEC = 90^{\circ}$，
∴$∠AEF + ∠DEC = 90^{\circ}$。
∵$∠ECD + ∠DEC = 90^{\circ}$，
∴$∠AEF = ∠ECD$。
在$△AEF$和$△DCE$中，
$\begin{cases}∠A = ∠D \\∠AEF = ∠DCE \\EF = EC\end{cases}$
∴$△AEF≌△DCE(AAS)$，
∴$AE = DC$。
设$AE = x$，则$DC = x$，$AD = AE + DE = x + 4$。
∵矩形$ABCD$的周长为$32cm$，
∴$2(AD + DC)=32$，即$AD + DC = 16$，
∴$x + 4 + x = 16$，
解得$x = 6$。
答：$AE$的长为$6cm$。

8. 若点$P关于x轴的对称点为P_1(2a + b,-a + 1)$,关于$y轴的对称点为P_2(4 - b,b + 2)$,则$a + b$的值是多少？

答案： 解：因为点P关于x轴的对称点为$P_1(2a + b,-a + 1)$，所以点P的坐标为$(2a + b,a - 1)$。
又因为点P关于y轴的对称点为$P_2(4 - b,b + 2)$，所以点P的坐标为$(b - 4,b + 2)$。
由此可得方程组：
$\begin{cases}2a + b = b - 4 \\a - 1 = b + 2\end{cases}$
解第一个方程：$2a + b = b - 4$，化简得$2a = -4$，解得$a = -2$。
将$a = -2$代入第二个方程：$-2 - 1 = b + 2$，即$-3 = b + 2$，解得$b = -5$。
所以$a + b = -2 + (-5) = -7$。
答：$a + b$的值是$-7$。

9. 某市广电局推出广电宽带上网业务,收费的方式有：
方案一：每月$80$元包月；
方案二：每月上网时间$x(\mathrm{h})与上网费用y$(元)的函数关系可用图中的折线表示；
方案三：以$0\mathrm{h}$为起点,每小时收费$1.6$元,月上网费用不超过$120$元,超过$120元的只收120$元。
(1)求方案二中$y与x的函数关系式(0\leqslant x\leqslant 100)$；
(2)试直接写出方案三中$y与x$的函数关系式；
(3)若一用户每月上网$60\mathrm{h}$,选用哪种方式上网最省钱？

答案：
(1) 当 $0 \leq x \leq 50$ 时，观察图像可知 $y = 58$；当 $50 ＜ x \leq 100$ 时，设 $y = kx + b$，将 $(50, 58)$ 和 $(100, 118)$ 代入得：$\begin{cases}50k + b = 58 \\ 100k + b = 118\end{cases}$，解得 $\begin{cases}k = \frac{6}{5} \\ b = -2\end{cases}$，所以 $y = \frac{6}{5}x - 2$。综上，$y=\left\{\begin{array}{l} 58(0\leqslant x\leqslant 50)\\ \frac {6}{5}x-2(50\lt x\leqslant 100)\end{array}\right.$
(2) 方案三每小时收费$1.6$元，当费用为$120$元时，上网时间为$120÷1.6 = 75$小时，所以 $y=\left\{\begin{array}{l} 1.6x(0\leqslant x\leqslant 75)\\ 120(x＞75)\end{array}\right.$
(3) 当上网$60$小时时，方案一费用为$80$元；方案二：$y = \frac{6}{5}×60 - 2 = 70$元；方案三：$y = 1.6×60 = 96$元。因为$70 ＜ 80 ＜ 96$，所以选用方案二最省钱。
(1) $y=\left\{\begin{array}{l} 58(0\leqslant x\leqslant 50)\\ \frac {6}{5}x-2(50\lt x\leqslant 100)\end{array}\right.$
(2) $y=\left\{\begin{array}{l} 1.6x(0\leqslant x\leqslant 75)\\ 120(x＞75)\end{array}\right.$
(3) 方案二