《2025年豫新锐暑假作业中原农民出版社八年级数学湘教版》

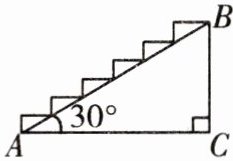
1. 如图,已知斜坡 $ AB $ 的长度是 $ 5 \mathrm{~m} $,点 $ A $ 与点 $ B $ 的水平距离是 $ 4.33 \mathrm{~m} $,$ \angle BAC = 30^{\circ} $。要为坡角为 $ 30^{\circ} $ 的楼梯表面铺地毯。地毯的长度为多少米？(精确到 $ 0.1 \mathrm{~m} $)

答案： 解：由题意得，△ABC是直角三角形，∠C=90°，∠BAC=30°，AB=5m，AC=4.33m。
因为在直角三角形中，30°角所对的直角边等于斜边的一半，所以BC=$\frac{1}{2}$AB=$\frac{1}{2}×5=2.5$m。
地毯的长度为水平总长与竖直总长之和，即AC+BC=4.33+2.5=6.83≈6.8m。
答：地毯的长度约为6.8米。

2. 如图,在 $ \mathrm{Rt} \triangle ABC $ 中,$ AB = AC $,$ \angle BAC = 90^{\circ} $。$ O $ 为 $ BC $ 的中点。
(1) 写出点 $ O $ 到 $ \triangle ABC $ 的三个顶点 $ A $,$ B $,$ C $ 的距离的关系(不要求说明理由)；
(2) 如果点 $ M $,$ N $ 分别在线段 $ AB $,$ AC $ 上移动,在移动中保持 $ AN = BM $,请判断 $ \triangle OMN $ 的形状,并说明理由。

答案：
(1)OA=OB=OC。
(2)△OMN为等腰直角三角形。理由如下：
∵AB=AC，∠BAC=90°，O为BC的中点，
∴OA=OB=OC，∠CAO=∠BAO=∠B=∠C=45°，AO⊥BC。
在△AON和△BOM中，
$\left\{\begin{array}{l} AN=BM,\\ ∠NAO=∠B,\\ AO=BO.\end{array}\right.$
∴△AON≌△BOM(SAS)，
∴ON=OM，∠NOA=∠MOB。
∴∠NOM=∠NOA+∠AOM=∠MOB+∠AOM=∠AOB=90°。
故△OMN为等腰直角三角形。

3. 小明、小华在一栋楼前感慨楼房真高。小明说：“这楼起码 20 层！”小华却不以为然：“20 层？我看没有,数数就知道了！”小明说：“有本事,你不用数也能明白！”小华想了想说：“没问题！让我们来量一量吧！”小明、小华在楼体两侧各选 $ A $,$ B $ 两点,测量数据如图,其中长方形 $ CDEF $ 表示楼体,$ AB = 150 \mathrm{~m} $,$ CD = 10 \mathrm{~m} $,$ \angle A = 30^{\circ} $,$ \angle B = 45^{\circ} $,$ A $,$ C $,$ D $,$ B $ 四点在同一直线上。问：

(1) 楼高多少米？
(2) 若每层楼按 $ 3 \mathrm{~m} $ 计算,你支持小明的观点还是小华的呢？请说明理由。(参考数据：$ \sqrt{3} \approx 1.73 $,$ \sqrt{2} \approx 1.41 $,$ \sqrt{5} \approx 2.24 $)

答案：
(1)解：设楼高为$x$米，则$CF = DE = x$。
因为$\angle A = 30^\circ$，$\angle ACF = 90^\circ$，所以在$Rt\triangle ACF$中，$\tan 30^\circ=\frac{CF}{AC}$，即$AC=\frac{CF}{\tan 30^\circ}=\frac{x}{\frac{\sqrt{3}}{3}}=\sqrt{3}x$。
因为$\angle B = 45^\circ$，$\angle BDE = 90^\circ$，所以在$Rt\triangle BDE$中，$\tan 45^\circ=\frac{DE}{BD}$，即$BD=\frac{DE}{\tan 45^\circ}=\frac{x}{1}=x$。
已知$AB = 150$米，$CD = 10$米，且$A$，$C$，$D$，$B$在同一直线上，所以$AC + CD + BD=AB$，即$\sqrt{3}x + 10 + x=150$。
整理得$(\sqrt{3}+1)x=140$，解得$x=\frac{140}{\sqrt{3}+1}=70(\sqrt{3}-1)$。
故楼高为$70(\sqrt{3}-1)$米。
(2)解：由
(1)得$x = 70(\sqrt{3}-1)$，$\sqrt{3}\approx1.73$，则$x\approx70×(1.73 - 1)=70×0.73 = 51.1$米。
每层楼按$3$米计算，$20$层楼的高度为$3×20 = 60$米。
因为$51.1\lt60$，所以支持小华的观点。