《2025年豫新锐暑假作业中原农民出版社八年级数学湘教版》

1. 如图,长方形 $ABCD$ 的长 $AD = 9$,宽 $AB = 3$,将其折叠,使点 $D$ 与点 $B$ 重合,那么折叠后 $DE$ 的长是______5.

答案： 5

2. 在 $\triangle ABC$ 中,$\angle C = 90^{\circ}$,周长为 $60$,斜边与一直角边长的比是 $13:5$,则这个三角形的三边长分别是(D)
A.$5$,$4$,$3$
B.$13$,$12$,$5$
C.$10$,$8$,$6$
D.$26$,$24$,$10$

答案： D

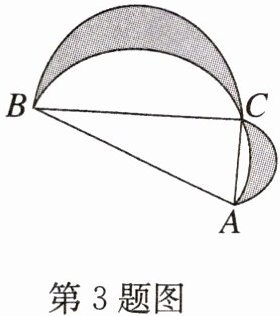
3. 如图,在 $Rt\triangle ABC$ 中,$AC = 10$,$BC = 24$,分别以它的三边为直径向上作三个半圆,则阴影部分的面积为______120.

答案： 120

4. 如图,在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,$BC = 6\ cm$,$AC = 8\ cm$. 按图中所示方法将 $\triangle BCD$ 沿 $BD$ 折叠,使点 $C$ 落在 $AB$ 边的点 $C'$ 处,那么 $\triangle ADC'$ 的面积是多少？

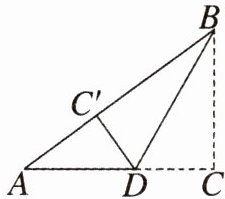
答案： 解：在$Rt\triangle ABC$中，$\angle C=90^{\circ}$，$BC=6\ cm$，$AC=8\ cm$，
由勾股定理得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{8^{2}+6^{2}}=10\ cm$。
由折叠性质得$BC'=BC=6\ cm$，$C'D=CD$，$\angle BC'D=\angle C=90^{\circ}$，
$\therefore AC'=AB-BC'=10-6=4\ cm$，$\angle AC'D=90^{\circ}$。
设$CD=C'D=x\ cm$，则$AD=AC-CD=(8-x)\ cm$。
在$Rt\triangle ADC'$中，由勾股定理得$AC'^{2}+C'D^{2}=AD^{2}$，
即$4^{2}+x^{2}=(8-x)^{2}$，
解得$x=3$。
$\therefore S_{\triangle ADC'}=\frac{1}{2}× AC'× C'D=\frac{1}{2}×4×3=6\ cm^{2}$。
答：$\triangle ADC'$的面积是$6\ cm^{2}$。

5. 小明在测学校旗杆的高度时发现旗杆上的绳子垂到地面还有 $1\ m$,当他把绳子拉直并把绳子的下端触地时,绳子下端离旗杆 $5\ m$,求旗杆的高度.

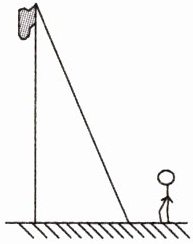
答案： 解:设旗杆高$x\ \text{m}$，则绳长$(x + 1)\ \text{m}$。
由勾股定理得：$x^{2}+5^{2}=(x + 1)^{2}$
展开方程：$x^{2}+25=x^{2}+2x + 1$
移项化简：$25 - 1=2x$
即：$24 = 2x$
解得：$x = 12$
答：旗杆的高度为$12\ \text{m}$。