2025年豫新锐暑假作业中原农民出版社八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年豫新锐暑假作业中原农民出版社八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
16. 为了了解八年级学生每周的课外阅读情况,某校语文组调查了该校八年级部分学生某周的课外阅读量 (精确到千字)。将调查数据经过统计整理后,得到如图的频数直方图,请根据该频数直方图,回答下列问题.

(1) 该校语文组调查了
(2) 估计被调查学生这一周的平均阅读量 (精确到千字).
解:$\frac{1}{40}×(4×6 + 6×9 + 10×12 + 12×15 + 8×18)$
$=\frac{1}{40}×(24 + 54 + 120 + 180 + 144)$
$=\frac{1}{40}×522$
$\approx13$(千字)
答:被调查学生这一周的平均阅读量约为13千字。

(1) 该校语文组调查了
40
名学生,左边第一组的频数为4
;(2) 估计被调查学生这一周的平均阅读量 (精确到千字).
解:$\frac{1}{40}×(4×6 + 6×9 + 10×12 + 12×15 + 8×18)$
$=\frac{1}{40}×(24 + 54 + 120 + 180 + 144)$
$=\frac{1}{40}×522$
$\approx13$(千字)
答:被调查学生这一周的平均阅读量约为13千字。
答案:
(1)40;4
(2)解:$\frac{1}{40}×(4×6 + 6×9 + 10×12 + 12×15 + 8×18)$
$=\frac{1}{40}×(24 + 54 + 120 + 180 + 144)$
$=\frac{1}{40}×522$
$\approx13$(千字)
答:被调查学生这一周的平均阅读量约为13千字。
(1)40;4
(2)解:$\frac{1}{40}×(4×6 + 6×9 + 10×12 + 12×15 + 8×18)$
$=\frac{1}{40}×(24 + 54 + 120 + 180 + 144)$
$=\frac{1}{40}×522$
$\approx13$(千字)
答:被调查学生这一周的平均阅读量约为13千字。
17. $5$ 月份,某品牌衬衣正式上市销售,$5$ 月 $1$ 日的销售量为 $10$ 件,$5$ 月 $2$ 日的销售量为 $35$ 件,以后每天的销售量比前一天多 $25$ 件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少 $15$ 件,直到 $5$ 月 $31$ 日销售量为 $0$. 设该品牌衬衣的日销售量为 $P$ (件),销售日期为 $n$ (日),$P$ 与 $n$ 之间的函数关系图象如图所示.
(1) 计算点 $B$ 的坐标.
(2) 写出 $P$ 关于 $n$ 的函数表达式 (注明 $n$ 的取值范围).
(3) 经研究表明,该品牌衬衣的日销售量超过 $150$ 件的时间为该品牌衬衣的流行期,则该品牌衬衣本月在市面的流行期是多少天?
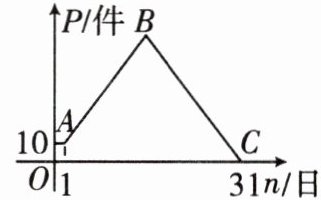
(1) 计算点 $B$ 的坐标.
(2) 写出 $P$ 关于 $n$ 的函数表达式 (注明 $n$ 的取值范围).
(3) 经研究表明,该品牌衬衣的日销售量超过 $150$ 件的时间为该品牌衬衣的流行期,则该品牌衬衣本月在市面的流行期是多少天?

答案:
解:
(1)设日销量逐渐增大一直到最大的天数是n,所以日销量逐渐减小到0的天数是31 - n,所以10+25(n - 1)=15(31 - n).解得n=12,15(31 - n)=285(件).所以点B的坐标为(12,285).
(2)设经过A,B两点的直线的表达式是P₁=k₁n+b₁(k₁≠0),经过B,C两点的直线的表达式是P₂=k₂n+b₂(k₂≠0).所以可得两个方程组{k₁+b₁=10,12k₁+b₁=285},{31k₂+b₂=0,12k₂+b₂=285},解得{k₁=25,b₁=-15},{k₂=-15,b₂=465}.所以函数表达式分别是P₁=25n - 15(n<12,n为正整数),P₂=-15n + 465(12≤n≤31,n为正整数).
(3)由题意,得{25n - 15>150,-15n + 465>150},解得6$\frac{3}{5}$<n<21.整数n的值可取7,8,9,...,20,共14个数,所以该品牌衬衣本月在市面的流行期是14天.
(1)设日销量逐渐增大一直到最大的天数是n,所以日销量逐渐减小到0的天数是31 - n,所以10+25(n - 1)=15(31 - n).解得n=12,15(31 - n)=285(件).所以点B的坐标为(12,285).
(2)设经过A,B两点的直线的表达式是P₁=k₁n+b₁(k₁≠0),经过B,C两点的直线的表达式是P₂=k₂n+b₂(k₂≠0).所以可得两个方程组{k₁+b₁=10,12k₁+b₁=285},{31k₂+b₂=0,12k₂+b₂=285},解得{k₁=25,b₁=-15},{k₂=-15,b₂=465}.所以函数表达式分别是P₁=25n - 15(n<12,n为正整数),P₂=-15n + 465(12≤n≤31,n为正整数).
(3)由题意,得{25n - 15>150,-15n + 465>150},解得6$\frac{3}{5}$<n<21.整数n的值可取7,8,9,...,20,共14个数,所以该品牌衬衣本月在市面的流行期是14天.
查看更多完整答案,请扫码查看


