第70页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
核心考点 1 牧民饮马问题
1. 如图,直线$l$是一条河,$P$,$Q$是两个村庄. 计划在$l$上的某处修建一个水泵站$M$,向$P$,$Q$两地供水. 现有如下四种铺设方案(图中实线表示铺设的管道),则所需管道最短的是(

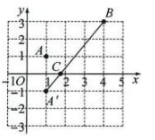
2. 如图,在平面直角坐标系中,已知$A(1,1)$,$B(4,3)$.
(1)$C$是$x$轴上的一个动点,当$AC + BC$的值最小时,在图中画出点$C$的位置.
(2)本题用到了哪些数学道理,请把它挑选出来并填在横线上:
①两点之间,线段最短;②线段垂直平分线上的点与这条线段两个端点的距离相等;
③角的平分线上的点到角两边的距离相等;④三角形两边之和大于第三边.

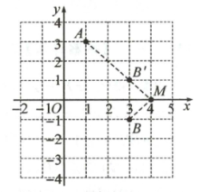
3. 如图,在平面直角坐标系中,已知点$A(1,3)$,$B(3,-1)$,$M$是$x$轴上一动点,当$AM - BM$的值最大时,在图中画出点$M$的位置,并写出点$M$的坐标:

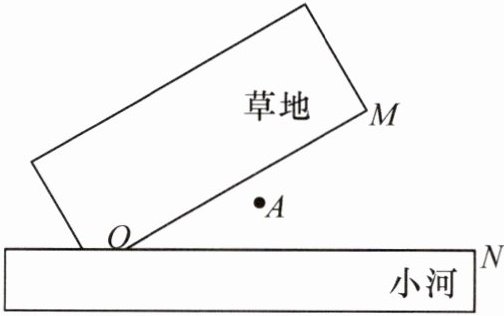
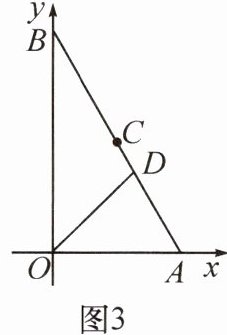
4. 如图,草地边缘$OM$与小河河岸$ON$在点$O$处形成$30^{\circ}$的夹角,牧马人从$A$地出发,先牵着马到草地吃草,然后再去河边饮水,最后回到$A$地. 已知$OA = 2\ km$,请在图中设计一条路线,使所走的路程最短,并求出整个过程所行走的路程.
核心考点 2 造桥选址问题
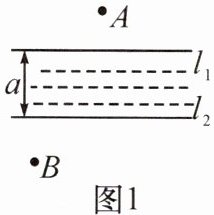
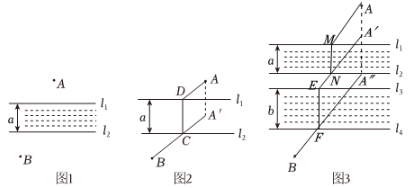
5. 如图 1,$A$,$B$两村之间有一条两岸互相平行的河,河宽为$a$. 现要在河上造一座桥(桥必须与河岸垂直),使$A$,$B$之间的路程最短,试画出造桥位置. 对于此题,我们可以这样解决:
如图 2,把点$A$向下平移河宽$a$到点$A'$,连接$A'B$交$l_{2}$于点$C$;过点$C$作$CD\perp l_{1}$于点$D$,则$CD$就是造桥位置.
请仿照以上材料,解决如下问题:
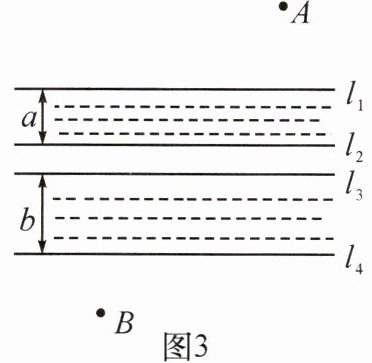
如图 3,$A$,$B$两村之间有两条互相平行的河. 一条河宽$a$,另一条河宽$b$,现欲在两条河上各造一座桥(桥必须与河岸垂直),使$A$,$B$之间的路程最短,试画出造桥位置.
6. 如图,一条东西流向的小河在点$G$和点$G'$处直角转弯,改变为南北流向,河宽不变. $A$,$B$两地分别在河的北岸和西岸,现要分别在东西、南北流向的河上建$CD$,$EF$两座桥,桥造在何处可使从$A$地到$B$地的路径$ACDEFB$最短?并说明理由.(假设河两岸是平行线,桥与河垂直)

综合应用
7. 综合实践:小明研究学习最短路径问题,发现可以根据“两点之间,线段最短”和“垂线段最短”探究“牧民饮马”和“造桥选址”两个问题,并初步运用探究经验解决线段和最小值的数学问题.
【问题探究】
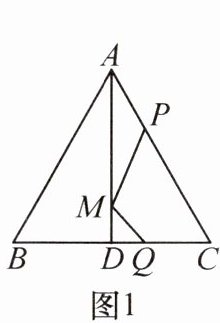
如图 1,在等边三角形$ABC$中,$D$为$BC$的中点,$P$,$Q$分别为$AC$,$BC$上的点,$AP = CQ = 2$,$DQ = 1$,$M$是线段$AD$上的动点,连接$MP$,$MQ$,求$MP + MQ$的最小值.
(1)小明提出的探究思路如下:如图 2,作点$Q$关于直线$AD$的对称点$Q'$,连接$PQ'$交$AD$于点$M$,连接$MQ$,根据“两点之间,线段最短”,可知此时$MP + MQ$的值最小.
①请你运用小明的探究思路,证明此时$MP + MQ$的值最小.
②求$MP + MQ$的最小值.
【类比探究】
(2)如图 3,在平面直角坐标系中,点$A$的坐标为$(4,0)$,$B$为$y$轴正半轴上一点,连接$AB$,$\angle ABO = 30^{\circ}$,$C$为$AB$的中点,$OD$平分$\angle AOB$交$AB$于点$D$,$P$为边$OB$上的一个动点. 若点$M$在线段$OD$上,连接$MC$,$MP$,则当$MC + MP$的值最小时,点$P$的坐标为

1. 如图,直线$l$是一条河,$P$,$Q$是两个村庄. 计划在$l$上的某处修建一个水泵站$M$,向$P$,$Q$两地供水. 现有如下四种铺设方案(图中实线表示铺设的管道),则所需管道最短的是(
D
)
2. 如图,在平面直角坐标系中,已知$A(1,1)$,$B(4,3)$.
(1)$C$是$x$轴上的一个动点,当$AC + BC$的值最小时,在图中画出点$C$的位置.
(2)本题用到了哪些数学道理,请把它挑选出来并填在横线上:
①②④
.(填序号)①两点之间,线段最短;②线段垂直平分线上的点与这条线段两个端点的距离相等;
③角的平分线上的点到角两边的距离相等;④三角形两边之和大于第三边.

3. 如图,在平面直角坐标系中,已知点$A(1,3)$,$B(3,-1)$,$M$是$x$轴上一动点,当$AM - BM$的值最大时,在图中画出点$M$的位置,并写出点$M$的坐标:
(4,0)
.
4. 如图,草地边缘$OM$与小河河岸$ON$在点$O$处形成$30^{\circ}$的夹角,牧马人从$A$地出发,先牵着马到草地吃草,然后再去河边饮水,最后回到$A$地. 已知$OA = 2\ km$,请在图中设计一条路线,使所走的路程最短,并求出整个过程所行走的路程.

核心考点 2 造桥选址问题
5. 如图 1,$A$,$B$两村之间有一条两岸互相平行的河,河宽为$a$. 现要在河上造一座桥(桥必须与河岸垂直),使$A$,$B$之间的路程最短,试画出造桥位置. 对于此题,我们可以这样解决:
如图 2,把点$A$向下平移河宽$a$到点$A'$,连接$A'B$交$l_{2}$于点$C$;过点$C$作$CD\perp l_{1}$于点$D$,则$CD$就是造桥位置.
请仿照以上材料,解决如下问题:
如图 3,$A$,$B$两村之间有两条互相平行的河. 一条河宽$a$,另一条河宽$b$,现欲在两条河上各造一座桥(桥必须与河岸垂直),使$A$,$B$之间的路程最短,试画出造桥位置.


6. 如图,一条东西流向的小河在点$G$和点$G'$处直角转弯,改变为南北流向,河宽不变. $A$,$B$两地分别在河的北岸和西岸,现要分别在东西、南北流向的河上建$CD$,$EF$两座桥,桥造在何处可使从$A$地到$B$地的路径$ACDEFB$最短?并说明理由.(假设河两岸是平行线,桥与河垂直)

综合应用
7. 综合实践:小明研究学习最短路径问题,发现可以根据“两点之间,线段最短”和“垂线段最短”探究“牧民饮马”和“造桥选址”两个问题,并初步运用探究经验解决线段和最小值的数学问题.
【问题探究】
如图 1,在等边三角形$ABC$中,$D$为$BC$的中点,$P$,$Q$分别为$AC$,$BC$上的点,$AP = CQ = 2$,$DQ = 1$,$M$是线段$AD$上的动点,连接$MP$,$MQ$,求$MP + MQ$的最小值.
(1)小明提出的探究思路如下:如图 2,作点$Q$关于直线$AD$的对称点$Q'$,连接$PQ'$交$AD$于点$M$,连接$MQ$,根据“两点之间,线段最短”,可知此时$MP + MQ$的值最小.
①请你运用小明的探究思路,证明此时$MP + MQ$的值最小.
②求$MP + MQ$的最小值.
【类比探究】
(2)如图 3,在平面直角坐标系中,点$A$的坐标为$(4,0)$,$B$为$y$轴正半轴上一点,连接$AB$,$\angle ABO = 30^{\circ}$,$C$为$AB$的中点,$OD$平分$\angle AOB$交$AB$于点$D$,$P$为边$OB$上的一个动点. 若点$M$在线段$OD$上,连接$MC$,$MP$,则当$MC + MP$的值最小时,点$P$的坐标为
①②
.


答案:
1.D
2.解:
(1)
(2)①②④
3.解:(4,0)
4.解:如图,分别作出点A关于OM,ON的对称点B,C,连接BC交OM,ON于点D,E,连接AD,AE,则线段AD,DE,EA即为所求路线.连接OB,OC.由作图可得,OB=OA=2 km,∠BOC=2∠MON=60°,BD=AD,EA=CE,
∴△OBC为等边三角形.
∴BC=OB=2 km.
∴AD+DE+EA=BD+DE+EC=BC=2 km,即整个过程所行走的路程为2 km.
5.解:
6.解:在点D,E处造桥DC,EF,所得路径ACDEFB最短.理由如下:把河的两岸看成平行线a,b和c,d,将AC沿与河岸垂直的方向平移等于河宽的距离,即点C移动到点D,点A移动到点A',则AA'=CD.同理,将BF沿与河岸垂直的方向平移等于河宽的距离,则BB'=EF.所以AC+DE+BF=A'D+DE+EB',当A',D,E,B'四点共线时,A'D+DE+EB'的值最小,为线段A'B'的长度.因此所得路径ACDEFB最短.
7.解:
(1)①证明:
∵△ABC是等边三角形,D为BC的中点,
∴AD⊥BC.
∵点Q,P关于直线AD对称,点P在线段AD上,
∴DQ=DQ,MQ=PM,QM=MQ.
∵点M为PQ的中点,
∴线段MQ,线段DQ,此时MP+MQ的值最小.②
∵AP=CQ=2,DQ=1,
∴DQ'=DQ=1,AC=BC=2CD=2×(2+1)=6,
∴PC+CQ=4.∠C=60°,
∴△PCQ是等边三角形,
∴PQ=PC=4,即MP+MQ的最小值为4.
(2)①②
1.D
2.解:
(1)

(2)①②④
3.解:(4,0)

4.解:如图,分别作出点A关于OM,ON的对称点B,C,连接BC交OM,ON于点D,E,连接AD,AE,则线段AD,DE,EA即为所求路线.连接OB,OC.由作图可得,OB=OA=2 km,∠BOC=2∠MON=60°,BD=AD,EA=CE,
∴△OBC为等边三角形.
∴BC=OB=2 km.
∴AD+DE+EA=BD+DE+EC=BC=2 km,即整个过程所行走的路程为2 km.
5.解:

6.解:在点D,E处造桥DC,EF,所得路径ACDEFB最短.理由如下:把河的两岸看成平行线a,b和c,d,将AC沿与河岸垂直的方向平移等于河宽的距离,即点C移动到点D,点A移动到点A',则AA'=CD.同理,将BF沿与河岸垂直的方向平移等于河宽的距离,则BB'=EF.所以AC+DE+BF=A'D+DE+EB',当A',D,E,B'四点共线时,A'D+DE+EB'的值最小,为线段A'B'的长度.因此所得路径ACDEFB最短.
7.解:
(1)①证明:
∵△ABC是等边三角形,D为BC的中点,
∴AD⊥BC.
∵点Q,P关于直线AD对称,点P在线段AD上,
∴DQ=DQ,MQ=PM,QM=MQ.
∵点M为PQ的中点,
∴线段MQ,线段DQ,此时MP+MQ的值最小.②
∵AP=CQ=2,DQ=1,
∴DQ'=DQ=1,AC=BC=2CD=2×(2+1)=6,
∴PC+CQ=4.∠C=60°,
∴△PCQ是等边三角形,
∴PQ=PC=4,即MP+MQ的最小值为4.
(2)①②
查看更多完整答案,请扫码查看


