12. (10分)某同学做一道题,已知两个多项式$A$,$B$,求$A - B$的值.他误将“$A - B$”看成“$A + B$”,经过正确计算得到的结果是$x^{2}+14x - 6$,其中$A = - 2x^{2}+5x - 1$.
(1)请你帮助这位同学求出正确的结果;
(2)若$x$是最大的负整数,求$A - 2B$的值.
(1)请你帮助这位同学求出正确的结果;
(2)若$x$是最大的负整数,求$A - 2B$的值.
答案:
(1)因为$A+B=x^{2}+14x-6,A=-2x^{2}+5x-1,$
所以$B=x^{2}+14x-6-(-2x^{2}+5x-1)=3x^{2}+9x-5$,所以$A-B=-2x^{2}+5x-1-(3x^{2}+9x-5)=-5x^{2}-4x+4.$
(2)因为$A=-2x^{2}+5x-1,B=3x^{2}+9x-5,$
所以$A-2B=-2x^{2}+5x-1-2(3x^{2}+9x-5)=-8x^{2}-13x+9.$
因为 x 是最大的负整数,所以$x=-1,$
所以$A-2B=-8x^{2}-13x+9=-8+13+9=14.$
(1)因为$A+B=x^{2}+14x-6,A=-2x^{2}+5x-1,$
所以$B=x^{2}+14x-6-(-2x^{2}+5x-1)=3x^{2}+9x-5$,所以$A-B=-2x^{2}+5x-1-(3x^{2}+9x-5)=-5x^{2}-4x+4.$
(2)因为$A=-2x^{2}+5x-1,B=3x^{2}+9x-5,$
所以$A-2B=-2x^{2}+5x-1-2(3x^{2}+9x-5)=-8x^{2}-13x+9.$
因为 x 是最大的负整数,所以$x=-1,$
所以$A-2B=-8x^{2}-13x+9=-8+13+9=14.$
13. (10分)某商场购进了$A$,$B$两种商品,其中$A种商品每件的进价比B$种商品每件的进价多20元,购进$A$种商品3件与购进$B$种商品4件的总价相同.
(1)求$A$,$B$两种商品每件的进价分别是多少元;
(2)该商场购进了$A$,$B$两种商品共100件,所用资金为6900元,出售时,两种商品按标价出售,$A种商品每件的利润率为25\%$,$B$种商品每件可获利15元.若两种商品全部售完,则商场共可获利多少元?
(3)在(2)的条件下,$A$商品按标价全部售出,$B$商品按标价先售出一部分后,余下的再按标价的九折售出,$A$,$B$两种商品全部售出,总获利比全部按标价售出获利少了150元,则$B$商品按标价售出多少件?
(1)求$A$,$B$两种商品每件的进价分别是多少元;
(2)该商场购进了$A$,$B$两种商品共100件,所用资金为6900元,出售时,两种商品按标价出售,$A种商品每件的利润率为25\%$,$B$种商品每件可获利15元.若两种商品全部售完,则商场共可获利多少元?
(3)在(2)的条件下,$A$商品按标价全部售出,$B$商品按标价先售出一部分后,余下的再按标价的九折售出,$A$,$B$两种商品全部售出,总获利比全部按标价售出获利少了150元,则$B$商品按标价售出多少件?
答案:
(1)设 A 种商品每件的进价是 x 元,则 B 种商品每件的进价是$(x-20)$元,
由题意,得$3x=4(x-20)$,解得$x=80,$
所以$80-20=60$(元).
答:A 种商品每件的进价是 80 元,B 种商品每件的进价是 60 元.
(2)设购进 A 种商品 a 件,则购进 B 种商品$(100-a)$件,
由题意,得$80a+60(100-a)=6900,$
解得$a=45$,所以$100-a=100-45=55,$
所以$80×25\% ×45+15×55=1725$(元).
答:全部售完共可获利 1725 元.
(3)设 B 商品按标价售出 b 件,
根据题意,得$(60+15)×(1-0.9)(55-b)=150,$
解得$b=35.$
答:B 商品按标价售出 35 件.
(1)设 A 种商品每件的进价是 x 元,则 B 种商品每件的进价是$(x-20)$元,
由题意,得$3x=4(x-20)$,解得$x=80,$
所以$80-20=60$(元).
答:A 种商品每件的进价是 80 元,B 种商品每件的进价是 60 元.
(2)设购进 A 种商品 a 件,则购进 B 种商品$(100-a)$件,
由题意,得$80a+60(100-a)=6900,$
解得$a=45$,所以$100-a=100-45=55,$
所以$80×25\% ×45+15×55=1725$(元).
答:全部售完共可获利 1725 元.
(3)设 B 商品按标价售出 b 件,
根据题意,得$(60+15)×(1-0.9)(55-b)=150,$
解得$b=35.$
答:B 商品按标价售出 35 件.
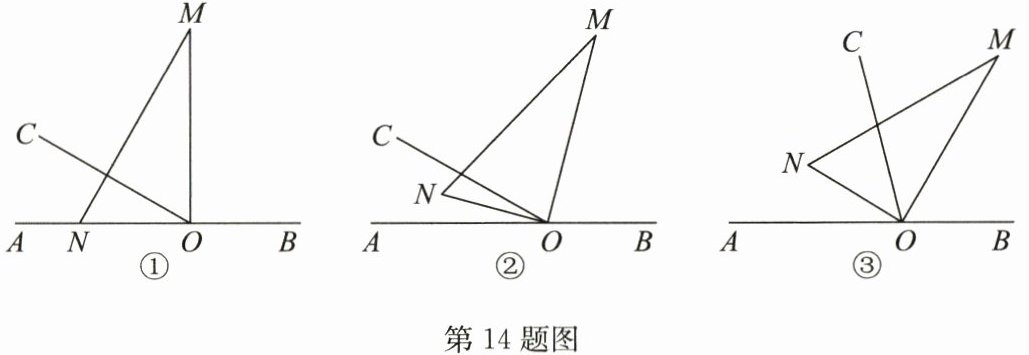
14. (10分)如图①,$O为直线AB$上一点,过点$O作射线OC$,$\angle AOC = 30^{\circ}$,将一直角三角尺的直角顶点放在点$O$处,一边$ON在射线OA$上,另一边$OM与OC都在直线AB$的上方.
(1)将图①中的三角尺绕点$O以每秒3^{\circ}$的速度顺时针旋转一周,经过$t$秒后,如图②,$OM恰好平分\angle BOC$,求$t$的值;
(2)在(1)的基础上,如果三角尺在转动的同时,射线$OC也绕点O以每秒6^{\circ}$的速度顺时针旋转一周(如图③),那么$t$的值为多少时,$OC平分\angle MON$?
(3)在(2)的基础上,$t$的值为多少时,$OC平分\angle MOB$?请画出图形并说明理由.
(1)将图①中的三角尺绕点$O以每秒3^{\circ}$的速度顺时针旋转一周,经过$t$秒后,如图②,$OM恰好平分\angle BOC$,求$t$的值;
(2)在(1)的基础上,如果三角尺在转动的同时,射线$OC也绕点O以每秒6^{\circ}$的速度顺时针旋转一周(如图③),那么$t$的值为多少时,$OC平分\angle MON$?
(3)在(2)的基础上,$t$的值为多少时,$OC平分\angle MOB$?请画出图形并说明理由.

答案:
(1)因为 OM 平分$∠BOC$,所以$∠COM=∠MOB=\frac {1}{2}∠BOC.$
因为$∠AOC=30^{\circ }$,所以$∠BOC=180^{\circ }-∠AOC=150^{\circ },$
所以$∠COM=75^{\circ }$,所以$∠CON=90^{\circ }-∠COM=15^{\circ },$
所以$∠AON=∠AOC-∠CON=30^{\circ }-15^{\circ }=15^{\circ },$
$t=15÷3=5$(秒).
(2)因为 OC 平分$∠MON,∠MON=90^{\circ },$
所以$∠CON=∠COM=45^{\circ }.$
当 OC 未停止运动时,设$∠AON=(3t)^{\circ }$,则$∠AOC=(30+6t)^{\circ }.$
因为$∠CON=∠AOC-∠AON=45^{\circ },$
所以$(30+6t)^{\circ }-(3t)^{\circ }=45^{\circ }$,解得$t=5.$
当 OC 停止运动时,因为 OC 平分$∠MON$,所以$∠AON=∠CON-∠AOC=45^{\circ }-30^{\circ }=15^{\circ },$
此时 ON 运动了$360^{\circ }-15^{\circ }=345^{\circ }$,所以$t=345÷3=115$(秒).
故当 t 的值为 5 或 115 时,OC 平分$∠MON.$
(3)画出图形如答图,

设$∠AON=(3t)^{\circ }$,则$∠AOC=(30+6t)^{\circ }.$
因为$∠MON=90^{\circ }$,所以$∠BOM+∠AON=90^{\circ },$
所以$∠BOM=90^{\circ }-∠AON=(90-3t)^{\circ }.$
因为 OC 平分$∠MOB,$
所以$∠BOC=∠COM=\frac {1}{2}∠BOM=\frac {1}{2}(90-3t)^{\circ },$
所以$180^{\circ }-(30+6t)^{\circ }=\frac {1}{2}(90-3t)^{\circ }$,解得$t=\frac {70}{3}.$
故当 t 的值为$\frac {70}{3}$时,OC 平分$∠MOB.$
(1)因为 OM 平分$∠BOC$,所以$∠COM=∠MOB=\frac {1}{2}∠BOC.$
因为$∠AOC=30^{\circ }$,所以$∠BOC=180^{\circ }-∠AOC=150^{\circ },$
所以$∠COM=75^{\circ }$,所以$∠CON=90^{\circ }-∠COM=15^{\circ },$
所以$∠AON=∠AOC-∠CON=30^{\circ }-15^{\circ }=15^{\circ },$
$t=15÷3=5$(秒).
(2)因为 OC 平分$∠MON,∠MON=90^{\circ },$
所以$∠CON=∠COM=45^{\circ }.$
当 OC 未停止运动时,设$∠AON=(3t)^{\circ }$,则$∠AOC=(30+6t)^{\circ }.$
因为$∠CON=∠AOC-∠AON=45^{\circ },$
所以$(30+6t)^{\circ }-(3t)^{\circ }=45^{\circ }$,解得$t=5.$
当 OC 停止运动时,因为 OC 平分$∠MON$,所以$∠AON=∠CON-∠AOC=45^{\circ }-30^{\circ }=15^{\circ },$
此时 ON 运动了$360^{\circ }-15^{\circ }=345^{\circ }$,所以$t=345÷3=115$(秒).
故当 t 的值为 5 或 115 时,OC 平分$∠MON.$
(3)画出图形如答图,

设$∠AON=(3t)^{\circ }$,则$∠AOC=(30+6t)^{\circ }.$
因为$∠MON=90^{\circ }$,所以$∠BOM+∠AON=90^{\circ },$
所以$∠BOM=90^{\circ }-∠AON=(90-3t)^{\circ }.$
因为 OC 平分$∠MOB,$
所以$∠BOC=∠COM=\frac {1}{2}∠BOM=\frac {1}{2}(90-3t)^{\circ },$
所以$180^{\circ }-(30+6t)^{\circ }=\frac {1}{2}(90-3t)^{\circ }$,解得$t=\frac {70}{3}.$
故当 t 的值为$\frac {70}{3}$时,OC 平分$∠MOB.$
查看更多完整答案,请扫码查看


