11. (10分)先化简,再求值:$5(3a^{2}b - ab^{2})-4(-ab^{2}+3a^{2}b)$,其中$a = 1,b = -2$.
答案:
解:原式=15a²b-5ab²+4ab²-12a²b=3a²b-ab².当a=1,b=-2时,原式=3×1²×(-2)-1×(-2)²=-6-4=-10.
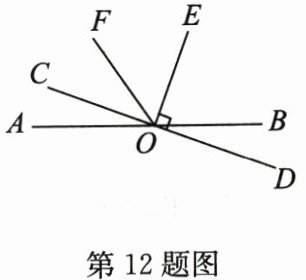
12. (10分)如图,直线$AB和CD相交于点O,OE\perp CD,OF平分\angle AOE$.
(1)$\angle AOC与\angle BOD$的大小关系是
(2)若$\angle COF = 35^{\circ}$,求$\angle BOD$的度数.
(1)$\angle AOC与\angle BOD$的大小关系是
$\angle AOC=\angle BOD$
,判断的依据是对顶角相等
;(2)若$\angle COF = 35^{\circ}$,求$\angle BOD$的度数.

解:
因为$OE\perp CD$,所以$\angle COE = 90^{\circ}$。
已知$\angle COF = 35^{\circ}$,则$\angle EOF=\angle COE-\angle COF$,即$\angle EOF = 90^{\circ}-35^{\circ}=55^{\circ}$。
因为$OF$平分$\angle AOE$,所以$\angle AOF=\angle EOF = 55^{\circ}$。
那么$\angle AOC=\angle AOF-\angle COF$,即$\angle AOC = 55^{\circ}-35^{\circ}=20^{\circ}$。
又因为$\angle AOC$与$\angle BOD$是对顶角,根据对顶角相等,所以$\angle BOD=\angle AOC = 20^{\circ}$。
因为$OE\perp CD$,所以$\angle COE = 90^{\circ}$。
已知$\angle COF = 35^{\circ}$,则$\angle EOF=\angle COE-\angle COF$,即$\angle EOF = 90^{\circ}-35^{\circ}=55^{\circ}$。
因为$OF$平分$\angle AOE$,所以$\angle AOF=\angle EOF = 55^{\circ}$。
那么$\angle AOC=\angle AOF-\angle COF$,即$\angle AOC = 55^{\circ}-35^{\circ}=20^{\circ}$。
又因为$\angle AOC$与$\angle BOD$是对顶角,根据对顶角相等,所以$\angle BOD=\angle AOC = 20^{\circ}$。
答案:
1. (1)
答案:$\angle AOC=\angle BOD$,对顶角相等。
2. (2)
解:
因为$OE\perp CD$,所以$\angle COE = 90^{\circ}$。
已知$\angle COF = 35^{\circ}$,则$\angle EOF=\angle COE-\angle COF$,即$\angle EOF = 90^{\circ}-35^{\circ}=55^{\circ}$。
因为$OF$平分$\angle AOE$,所以$\angle AOF=\angle EOF = 55^{\circ}$。
那么$\angle AOC=\angle AOF-\angle COF$,即$\angle AOC = 55^{\circ}-35^{\circ}=20^{\circ}$。
又因为$\angle AOC$与$\angle BOD$是对顶角,根据对顶角相等,所以$\angle BOD=\angle AOC = 20^{\circ}$。
综上,(1)$\angle AOC=\angle BOD$,对顶角相等;(2)$\angle BOD$的度数为$20^{\circ}$。
答案:$\angle AOC=\angle BOD$,对顶角相等。
2. (2)
解:
因为$OE\perp CD$,所以$\angle COE = 90^{\circ}$。
已知$\angle COF = 35^{\circ}$,则$\angle EOF=\angle COE-\angle COF$,即$\angle EOF = 90^{\circ}-35^{\circ}=55^{\circ}$。
因为$OF$平分$\angle AOE$,所以$\angle AOF=\angle EOF = 55^{\circ}$。
那么$\angle AOC=\angle AOF-\angle COF$,即$\angle AOC = 55^{\circ}-35^{\circ}=20^{\circ}$。
又因为$\angle AOC$与$\angle BOD$是对顶角,根据对顶角相等,所以$\angle BOD=\angle AOC = 20^{\circ}$。
综上,(1)$\angle AOC=\angle BOD$,对顶角相等;(2)$\angle BOD$的度数为$20^{\circ}$。
13. (10分)某单位计划购进一批手写板,网上某店铺的标价为900元/台,优惠活动如下表:

(1)①若该单位购买了16台这种手写板,需要花
②若该单位购买了$x(x>20)$台这种手写板,需要花
(2)若该单位购买的这种手写板的均价为696元/台,求该单位购买的数量.
解:设该单位购买了x台手写板.当0<x≤10时,均价为760元/台,不合题意;
当10<x≤20时,单位花了10×(900-140)+(x-10)×(900-220)=(680x+800)元,
所以680x+800=696x,解得x=50(不符合题意).
当x>20时,600x+2400=696x,
解得x=25.
答:该单位购买了25台手写板.

(1)①若该单位购买了16台这种手写板,需要花
11680
元;②若该单位购买了$x(x>20)$台这种手写板,需要花
(600x+2400)
元.(用含$x$的代数式表示)(2)若该单位购买的这种手写板的均价为696元/台,求该单位购买的数量.
解:设该单位购买了x台手写板.当0<x≤10时,均价为760元/台,不合题意;
当10<x≤20时,单位花了10×(900-140)+(x-10)×(900-220)=(680x+800)元,
所以680x+800=696x,解得x=50(不符合题意).
当x>20时,600x+2400=696x,
解得x=25.
答:该单位购买了25台手写板.
答案:
(1)①11680 ②(600x+2400)
(2)解:设该单位购买了x台手写板.当0<x≤10时,均价为760元/台,不合题意;
当10<x≤20时,单位花了10×(900-140)+(x-10)×(900-220)=(680x+800)元,
所以680x+800=696x,解得x=50(不符合题意).
当x>20时,600x+2400=696x,
解得x=25.
答:该单位购买了25台手写板.
(1)①11680 ②(600x+2400)
(2)解:设该单位购买了x台手写板.当0<x≤10时,均价为760元/台,不合题意;
当10<x≤20时,单位花了10×(900-140)+(x-10)×(900-220)=(680x+800)元,
所以680x+800=696x,解得x=50(不符合题意).
当x>20时,600x+2400=696x,
解得x=25.
答:该单位购买了25台手写板.
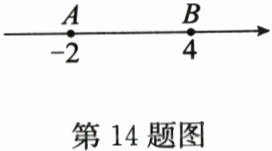
14. (10分)如图,数轴上有两个点$A,B$,表示的数分别是$-2,4$.请回答以下问题:
(1)点$A与点B$之间的距离为
(2)若点$P从点A$出发,以每秒5个单位长度的速度向右做匀速运动,点$Q从点B$出发,以每秒3个单位长度的速度向右做匀速运动,$P,Q$两点同时运动,设运动时间为$t$秒.
①当点$P$运动多少秒时,点$P和点Q$重合?
②当点$P$运动多少秒时,点$P,Q$之间的距离为3个单位长度?
(1)点$A与点B$之间的距离为
6
.(2)若点$P从点A$出发,以每秒5个单位长度的速度向右做匀速运动,点$Q从点B$出发,以每秒3个单位长度的速度向右做匀速运动,$P,Q$两点同时运动,设运动时间为$t$秒.
①当点$P$运动多少秒时,点$P和点Q$重合?
②当点$P$运动多少秒时,点$P,Q$之间的距离为3个单位长度?

①3秒;②$\frac{3}{2}$秒或$\frac{9}{2}$秒
答案:
1. (1)
根据数轴上两点间距离公式$d = |x_2 - x_1|$($x_1,x_2$为两点所表示的数),已知$A$表示$-2$,$B$表示$4$,则$AB=|4 - (-2)|=|4 + 2| = 6$。
2. (2)
①
解:$t$秒后,点$P$表示的数为$-2 + 5t$,点$Q$表示的数为$4+3t$。
当$P$和$Q$重合时,$-2 + 5t=4 + 3t$。
移项可得:$5t-3t=4 + 2$。
合并同类项:$2t=6$。
解得$t = 3$。
②
解:分两种情况讨论。
情况一:$P$在$Q$左侧时,$(4 + 3t)-(-2 + 5t)=3$。
去括号得:$4 + 3t + 2-5t=3$。
移项得:$3t-5t=3-(4 + 2)$。
合并同类项得:$-2t=3 - 6=-3$。
解得$t=\frac{3}{2}$。
情况二:$P$在$Q$右侧时,$(-2 + 5t)-(4 + 3t)=3$。
去括号得:$-2 + 5t-4-3t=3$。
移项得:$5t-3t=3 + 2 + 4$。
合并同类项得:$2t=9$。
解得$t=\frac{9}{2}$。
综上,(1)$6$;(2)①$3$秒;②$\frac{3}{2}$秒或$\frac{9}{2}$秒。
根据数轴上两点间距离公式$d = |x_2 - x_1|$($x_1,x_2$为两点所表示的数),已知$A$表示$-2$,$B$表示$4$,则$AB=|4 - (-2)|=|4 + 2| = 6$。
2. (2)
①
解:$t$秒后,点$P$表示的数为$-2 + 5t$,点$Q$表示的数为$4+3t$。
当$P$和$Q$重合时,$-2 + 5t=4 + 3t$。
移项可得:$5t-3t=4 + 2$。
合并同类项:$2t=6$。
解得$t = 3$。
②
解:分两种情况讨论。
情况一:$P$在$Q$左侧时,$(4 + 3t)-(-2 + 5t)=3$。
去括号得:$4 + 3t + 2-5t=3$。
移项得:$3t-5t=3-(4 + 2)$。
合并同类项得:$-2t=3 - 6=-3$。
解得$t=\frac{3}{2}$。
情况二:$P$在$Q$右侧时,$(-2 + 5t)-(4 + 3t)=3$。
去括号得:$-2 + 5t-4-3t=3$。
移项得:$5t-3t=3 + 2 + 4$。
合并同类项得:$2t=9$。
解得$t=\frac{9}{2}$。
综上,(1)$6$;(2)①$3$秒;②$\frac{3}{2}$秒或$\frac{9}{2}$秒。
查看更多完整答案,请扫码查看


