10. (10分)解方程:
(1)$5x + 1 = 3(x - 1) + 4$; (2)$\frac{3x - 2}{4} - \frac{5x - 7}{6} = 1$.
(1)$5x + 1 = 3(x - 1) + 4$; (2)$\frac{3x - 2}{4} - \frac{5x - 7}{6} = 1$.
答案:
$(1)$ 解方程$5x + 1 = 3(x - 1) + 4$
解:
去括号得:$5x + 1 = 3x - 3 + 4$
移项得:$5x - 3x = -3 + 4 - 1$
合并同类项得:$2x = 0$
系数化为$1$得:$x = 0$
$(2)$ 解方程$\frac{3x - 2}{4} - \frac{5x - 7}{6} = 1$
解:
去分母(方程两边同时乘以$12$)得:$12×\frac{3x - 2}{4} - 12×\frac{5x - 7}{6} = 12×1$
即$3(3x - 2) - 2(5x - 7) = 12$
去括号得:$9x - 6 - 10x + 14 = 12$
移项得:$9x - 10x = 12 + 6 - 14$
合并同类项得:$-x = 4$
系数化为$1$得:$x = -4$
综上,$(1)$中方程的解为$x = 0$;$(2)$中方程的解为$x = -4$。
解:
去括号得:$5x + 1 = 3x - 3 + 4$
移项得:$5x - 3x = -3 + 4 - 1$
合并同类项得:$2x = 0$
系数化为$1$得:$x = 0$
$(2)$ 解方程$\frac{3x - 2}{4} - \frac{5x - 7}{6} = 1$
解:
去分母(方程两边同时乘以$12$)得:$12×\frac{3x - 2}{4} - 12×\frac{5x - 7}{6} = 12×1$
即$3(3x - 2) - 2(5x - 7) = 12$
去括号得:$9x - 6 - 10x + 14 = 12$
移项得:$9x - 10x = 12 + 6 - 14$
合并同类项得:$-x = 4$
系数化为$1$得:$x = -4$
综上,$(1)$中方程的解为$x = 0$;$(2)$中方程的解为$x = -4$。
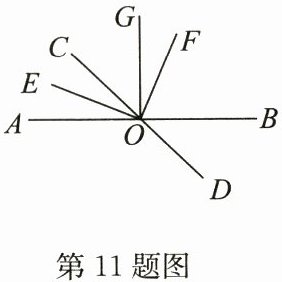
11. (12分)如图,直线$AB,CD相交于点O$,$OE平分∠AOC$,$OF平分∠BOC$,$OG⊥AB$.
(1)请判断$OE与OF$的位置关系,并说明理由;
(2)若$∠BOF - ∠COG = 22^{\circ}$,求$∠BOD$的度数.
(1)请判断$OE与OF$的位置关系,并说明理由;
(2)若$∠BOF - ∠COG = 22^{\circ}$,求$∠BOD$的度数.

答案:
解:
(1)OE⊥OF.理由如下:
因为OE平分∠AOC,所以∠EOC=$\frac{1}{2}$∠AOC.
因为OF平分∠BOC,所以∠COF=$\frac{1}{2}$∠BOC.
因为∠AOC+∠BOC=180°,
所以∠EOF=∠EOC+∠COF=$\frac{1}{2}$(∠AOC+∠BOC)=90°,所以OE⊥OF.
(2)因为OG⊥AB,所以∠AOG=∠BOG=90°.
设∠AOE=x,则∠AOC=2x,所以∠COG=90°-2x.
因为∠EOF=90°,所以∠BOF=90°-x.
因为∠BOF-∠COG=22°,
所以(90°-x)-(90°-2x)=22°,解得x=22°,
所以∠BOD=∠AOC=2x=44°.
(1)OE⊥OF.理由如下:
因为OE平分∠AOC,所以∠EOC=$\frac{1}{2}$∠AOC.
因为OF平分∠BOC,所以∠COF=$\frac{1}{2}$∠BOC.
因为∠AOC+∠BOC=180°,
所以∠EOF=∠EOC+∠COF=$\frac{1}{2}$(∠AOC+∠BOC)=90°,所以OE⊥OF.
(2)因为OG⊥AB,所以∠AOG=∠BOG=90°.
设∠AOE=x,则∠AOC=2x,所以∠COG=90°-2x.
因为∠EOF=90°,所以∠BOF=90°-x.
因为∠BOF-∠COG=22°,
所以(90°-x)-(90°-2x)=22°,解得x=22°,
所以∠BOD=∠AOC=2x=44°.
12. (12分)一辆卡车从$A地出发匀速开往B$地,速度为40千米/时,卡车出发2小时后,一辆出租车从$B地出发匀速开往A$地,卡车出发6小时,两车同时到达各自的目的地(到达目的地后两车都停止行驶).
(1)出租车的速度为
(2)设卡车行驶$x$小时,用含$x$的代数式表示两车行驶的路程之和;
(3)当两车相距180千米时,求卡车行驶的时间.
(1)出租车的速度为
60
千米/时;(2)设卡车行驶$x$小时,用含$x$的代数式表示两车行驶的路程之和;
解:出租车未出发时,即当0≤x≤2时,
路程和为40x千米;
出租车出发后,即当2<x≤6时,
路程和为40x+60(x-2)=(100x-120)千米.
答:两车行驶的路程之和为40x千米或(100x-120)千米.
路程和为40x千米;
出租车出发后,即当2<x≤6时,
路程和为40x+60(x-2)=(100x-120)千米.
答:两车行驶的路程之和为40x千米或(100x-120)千米.
(3)当两车相距180千米时,求卡车行驶的时间.
解:出租车未出发时:40x=40×6-180,解得x=1.5;
出租车出发后:40x+60(x-2)=40×6+180,
解得x=5.4.
答:卡车行驶的时间为1.5小时或5.4小时.
出租车出发后:40x+60(x-2)=40×6+180,
解得x=5.4.
答:卡车行驶的时间为1.5小时或5.4小时.
答案:
(1)60
(2)解:出租车未出发时,即当0≤x≤2时,
路程和为40x千米;
出租车出发后,即当2<x≤6时,
路程和为40x+60(x-2)=(100x-120)千米.
答:两车行驶的路程之和为40x千米或(100x-120)千米.
(3)解:出租车未出发时:40x=40×6-180,解得x=1.5;
出租车出发后:40x+60(x-2)=40×6+180,
解得x=5.4.
答:卡车行驶的时间为1.5小时或5.4小时.
(1)60
(2)解:出租车未出发时,即当0≤x≤2时,
路程和为40x千米;
出租车出发后,即当2<x≤6时,
路程和为40x+60(x-2)=(100x-120)千米.
答:两车行驶的路程之和为40x千米或(100x-120)千米.
(3)解:出租车未出发时:40x=40×6-180,解得x=1.5;
出租车出发后:40x+60(x-2)=40×6+180,
解得x=5.4.
答:卡车行驶的时间为1.5小时或5.4小时.
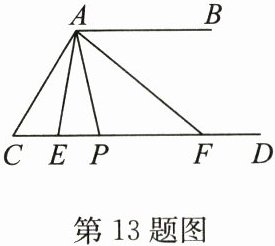
13. (12分)如图,$AB// CD$,$P是射线CD$上一个动点(点$P不与点C$重合),$∠CAP和∠BAP的平分线AE,AF分别交射线CD于点E,F$.
(1)若$∠C = 50^{\circ}$,求$∠EAF$的度数;
(2)无论点$P运动到射线CD$上的任意位置(点$P不与点C$重合),$∠CPA和∠CFA$都保持不变的数量关系,写出两者之间的数量关系,并说明理由.
(1)若$∠C = 50^{\circ}$,求$∠EAF$的度数;
(2)无论点$P运动到射线CD$上的任意位置(点$P不与点C$重合),$∠CPA和∠CFA$都保持不变的数量关系,写出两者之间的数量关系,并说明理由.

答案:
解:
(1)因为AB//CD,所以∠C+∠BAC=180°.
因为∠C=50°,所以∠BAC=130°.
因为AE,AF分别平分∠CAP和∠BAP,
所以∠PAE=$\frac{1}{2}$∠PAC,∠PAF=$\frac{1}{2}$∠BAP,
所以∠PAE+∠PAF=$\frac{1}{2}$(∠PAC+∠PAB),
所以∠EAF=$\frac{1}{2}$∠BAC=65°.
(2)∠CPA=2∠CFA,理由如下:
因为AB//CD,所以∠CFA=∠BAF,∠CPA=∠PAB.
因为AF平分∠PAB,所以∠PAB=2∠FAB,
所以∠CPA=2∠CFA.
(1)因为AB//CD,所以∠C+∠BAC=180°.
因为∠C=50°,所以∠BAC=130°.
因为AE,AF分别平分∠CAP和∠BAP,
所以∠PAE=$\frac{1}{2}$∠PAC,∠PAF=$\frac{1}{2}$∠BAP,
所以∠PAE+∠PAF=$\frac{1}{2}$(∠PAC+∠PAB),
所以∠EAF=$\frac{1}{2}$∠BAC=65°.
(2)∠CPA=2∠CFA,理由如下:
因为AB//CD,所以∠CFA=∠BAF,∠CPA=∠PAB.
因为AF平分∠PAB,所以∠PAB=2∠FAB,
所以∠CPA=2∠CFA.
查看更多完整答案,请扫码查看


