《2025年启东中学作业本七年级数学上册苏科版徐州专版》

18. (8分)如图,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成正方体的不同的表面展开图(填出两种互不相同的答案)。

答案：
解:如答图(答案不唯一).　　　　

19. (8分)如图,上面的图形分别是下面哪个立体图形展开的形状？请你把有对应关系的平面图形与立体图形连接起来。

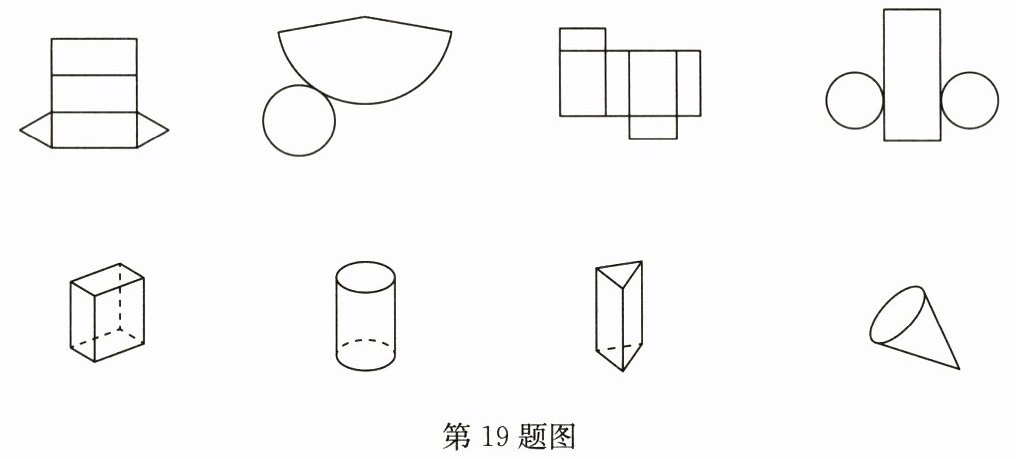
答案：
解:如答图所示.　

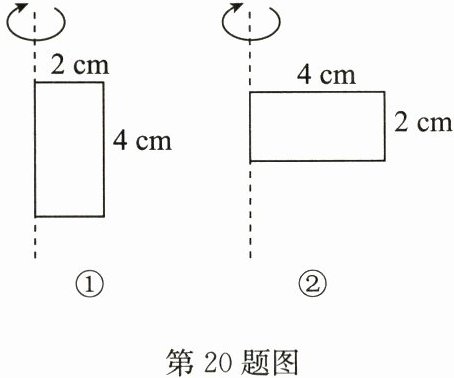
20. (10分)如图,将长和宽分别为4cm和2cm的长方形分别绕图①,②中的虚线轴旋转一周得到两个几何体,所得两个几何体的体积相等吗？如果不相等,哪一个体积较大？

答案： 解:对于题图①，旋转一周得到的几何体体积为$\pi× 2^2×4=16\pi(\text{cm}^3)$.　　对于题图②，旋转一周得到的几何体体积为$\pi×4^2× 2=32\pi(\text{cm}^3)$.　　因为$16\pi＜32\pi$，所以两个几何体的体积不相等，题图②得到的几何体的体积较大.

21. (10分)小明同学将一个长方体包装盒展开,进行了测量,结果如图所示。
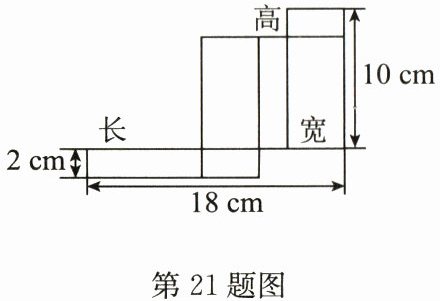
(1)该长方体包装盒的长为8cm,宽为4cm,高为2cm；
(2)求这个长方体包装盒的表面积和体积。

(2)解:表面积为$2×(8×4+8×2+4×2)=2×(32+16+8)=2×56=112(\text{cm}^2)$,　　体积为$8×4×2=64(\text{cm}^3)$.　　答:这个长方体包装盒的表面积为112$\text{cm}^2$，体积为64$\text{cm}^3$.

答案：
(1)8　4　2 　　
(2)解:表面积为$2×(8×4+8×2+4×2)=2×(32+16+8)=2×56=112(\text{cm}^2)$,　　体积为$8×4×2=64(\text{cm}^3)$.　　答:这个长方体包装盒的表面积为112$\text{cm}^2$，体积为64$\text{cm}^3$.