22. (12分)如图①是一个边长为10cm的正方形。
(1)如图②,若将该正方形沿粗黑实线剪下4个边长为
(2)若该正方形是一个圆柱的侧面展开图,求该圆柱的体积。(结果保留$\pi$)
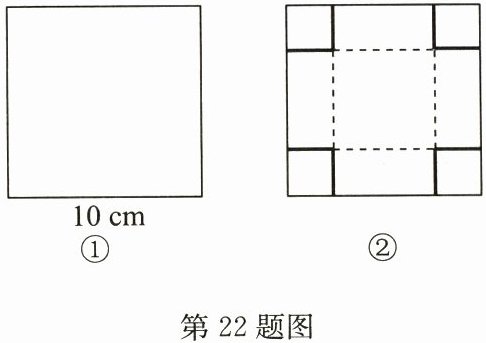
(1)如图②,若将该正方形沿粗黑实线剪下4个边长为
2.5
cm的小正方形,拼成一个大正方形作为长方体的一个底面,余下部分按虚线折叠成一个无盖的长方体盒子,最后把两部分拼在一起,组成一个完整的长方体,它的表面积等于原正方形的面积;(2)若该正方形是一个圆柱的侧面展开图,求该圆柱的体积。(结果保留$\pi$)

(2)解:因为正方形的边长为10$\text{cm}$, 所以圆柱的底面圆半径是$\frac{10}{\pi}×\frac{1}{2}=\frac{5}{\pi}(\text{cm})$, 所以圆柱的体积是$\pi\cdot\left(\frac{5}{\pi}\right)^2\cdot10=\frac{250}{\pi}(\text{cm}^3)$. 答:该圆柱的体积是$\frac{250}{\pi}\text{cm}^3$.
答案:
(1)2.5
(2)解:因为正方形的边长为10$\text{cm}$, 所以圆柱的底面圆半径是$\frac{10}{\pi}×\frac{1}{2}=\frac{5}{\pi}(\text{cm})$, 所以圆柱的体积是$\pi\cdot\left(\frac{5}{\pi}\right)^2\cdot10=\frac{250}{\pi}(\text{cm}^3)$. 答:该圆柱的体积是$\frac{250}{\pi}\text{cm}^3$.
(1)2.5
(2)解:因为正方形的边长为10$\text{cm}$, 所以圆柱的底面圆半径是$\frac{10}{\pi}×\frac{1}{2}=\frac{5}{\pi}(\text{cm})$, 所以圆柱的体积是$\pi\cdot\left(\frac{5}{\pi}\right)^2\cdot10=\frac{250}{\pi}(\text{cm}^3)$. 答:该圆柱的体积是$\frac{250}{\pi}\text{cm}^3$.
23. (14分)(1)如图,补全图形,使之成为长方体$ABCD - A_1B_1C_1D_1$的直观图(不必写画法);
(2)结合图形,回答下列问题:
与棱AB垂直的平面有______个;这个长方体所有棱长的和为36cm,如果长比高多1cm,宽比高少1cm,那么这个长方体的高是______cm。
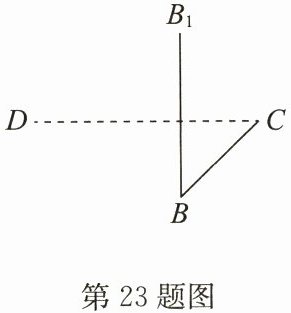
(2)结合图形,回答下列问题:
与棱AB垂直的平面有______个;这个长方体所有棱长的和为36cm,如果长比高多1cm,宽比高少1cm,那么这个长方体的高是______cm。

答案:
(1)解:补全图形如答图.
(2)2 3
(1)解:补全图形如答图.

(2)2 3
24. (14分)如图所示的几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律。
(1)第1个几何体中只有2个面涂色的小立方体共有
(2)第n个几何体中只有2个面涂色的小立方体共有
(1)第1个几何体中只有2个面涂色的小立方体共有
4
个,第2个几何体中只有2个面涂色的小立方体共有12
个,第3个几何体中只有2个面涂色的小立方体共有20
个,第10个几何体中只有2个面涂色的小立方体共有76
个;(2)第n个几何体中只有2个面涂色的小立方体共有
(8n-4)
个。(用含n的式子表示)
答案:
(1)4 12 20 76
(2)$(8n-4)$
(1)4 12 20 76
(2)$(8n-4)$
查看更多完整答案,请扫码查看


