《2025年启东中学作业本七年级数学上册苏科版徐州专版》

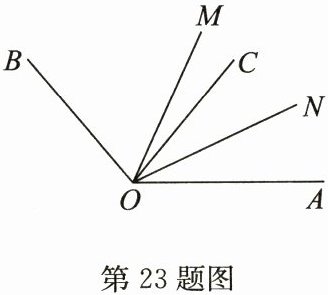
23. (10分)如图,射线OC在∠AOB的内部,OM,ON分别是∠AOB,∠AOC的平分线.
(1)如果∠AOB= 140°,∠AOC= 60°,那么∠MON的度数是多少?
(2)请写出∠MON与∠BOC的数量关系,并说明理由.

答案： 1. （1）
解：
因为$OM$是$\angle AOB$的平分线，$\angle AOB = 140^{\circ}$，根据角平分线定义$\angle AOM=\frac{1}{2}\angle AOB$。
所以$\angle AOM=\frac{1}{2}×140^{\circ}=70^{\circ}$。
又因为$ON$是$\angle AOC$的平分线，$\angle AOC = 60^{\circ}$，根据角平分线定义$\angle AON=\frac{1}{2}\angle AOC$。
所以$\angle AON=\frac{1}{2}×60^{\circ}=30^{\circ}$。
则$\angle MON=\angle AOM - \angle AON$。
把$\angle AOM = 70^{\circ}$，$\angle AON = 30^{\circ}$代入可得$\angle MON=70^{\circ}-30^{\circ}=40^{\circ}$。
2. （2）
解：
设$\angle AOC = 2x$，$\angle BOC = 2y$，则$\angle AOB=\angle AOC+\angle BOC=2x + 2y$。
因为$OM$是$\angle AOB$的平分线，所以$\angle AOM=\frac{1}{2}\angle AOB=\frac{1}{2}(2x + 2y)=x + y$。
因为$ON$是$\angle AOC$的平分线，所以$\angle AON=\frac{1}{2}\angle AOC=x$。
那么$\angle MON=\angle AOM-\angle AON$。
把$\angle AOM=x + y$，$\angle AON = x$代入可得$\angle MON=(x + y)-x=y$。
而$\angle BOC = 2y$，所以$\angle MON=\frac{1}{2}\angle BOC$。
综上，（1）$\angle MON$的度数是$40^{\circ}$；（2）$\angle MON$与$\angle BOC$的数量关系是$\angle MON=\frac{1}{2}\angle BOC$。

24. (10分)如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
(1)图中∠AOF的余角是∠AOD，∠EOF;(把符合条件的角都填出来)
(2)图中除直角相等外,还有相等的角,请写出三对;
∠AOC=∠BOD，∠AOE=∠COF，∠EOF=∠AOC
(3)①如果∠AOD= 140°,那么根据对顶角相等,可得∠BOC的度数是140°;
②如果∠EOF= 1/5∠AOD,求∠EOF的度数.
解：因为OE⊥AB，OF⊥CD，所以∠AOE=∠COF=90°。
则∠EOF+∠AOF=∠AOC+∠AOF=90°，所以∠EOF=∠AOC。
又因为∠AOC+∠AOD=180°（邻补角定义），设∠EOF=x，则∠AOD=5x。
由x+5x=180°，解得x=30°。
所以∠EOF的度数是30°。

答案： 1. （1）
因为$OF\perp CD$，所以$\angle FOD = 90^{\circ}$，$\angle AOF+\angle AOD = 90^{\circ}$；又因为$OE\perp AB$，$\angle AOE = 90^{\circ}$，$\angle AOF+\angle EOF=90^{\circ}$。
所以$\angle AOF$的余角是$\angle AOD$，$\angle EOF$。
2. （2）
相等的角：$\angle AOC=\angle AOD$（对顶角相等）；$\angle AOE=\angle COF = 90^{\circ}$（垂直定义）；$\angle EOF=\angle AOC$（因为$\angle AOC+\angle AOD = 90^{\circ}$，$\angle EOF+\angle AOF = 90^{\circ}$，$\angle AOF+\angle AOD = 90^{\circ}$，所以$\angle EOF=\angle AOC$）。
3. （3）
①
如果$\angle AOD = 140^{\circ}$，那么根据对顶角相等，可得$\angle BOC$的度数是$140^{\circ}$。
②
解：因为$OE\perp AB$，$OF\perp CD$，所以$\angle AOE=\angle COF = 90^{\circ}$。
则$\angle EOF+\angle AOF=\angle AOC+\angle AOF = 90^{\circ}$，所以$\angle EOF=\angle AOC$。
又因为$\angle AOC+\angle AOD = 180^{\circ}$（邻补角定义），设$\angle EOF=x$，则$\angle AOD = 5x$。
由$\angle EOF+\angle AOD=180^{\circ}$（$\angle AOC$与$\angle AOD$互补，$\angle EOF = \angle AOC$），即$x + 5x=180^{\circ}$。
合并同类项得$6x = 180^{\circ}$，解得$x = 30^{\circ}$。
所以$\angle EOF$的度数是$30^{\circ}$。
综上，答案依次为：（1）$\angle AOD$，$\angle EOF$；（2）$\angle AOC=\angle AOD$，$\angle AOE=\angle COF$，$\angle EOF=\angle AOC$（答案不唯一）；（3）①对顶角相等，$140^{\circ}$；②$30^{\circ}$。

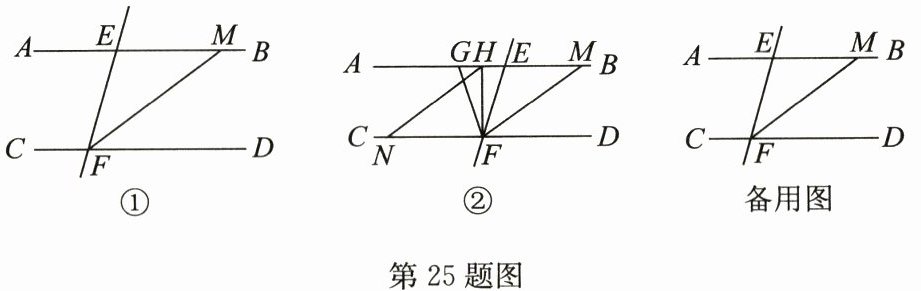
25. (12分)如图①,直线EF与直线AB交于点E,与直线CD交于点F,FM平分∠EFD交直线AB于点M,∠EFM= ∠EMF.
(1)试判断直线AB与CD的位置关系,并说明理由;
(2)G是射线MA上的一个动点(不与点M,E重合),FH平分∠EFG交直线AB于点H,过点H作HN//FM交直线CD于点N.设∠FHN= α,∠FGE= β.
①如图②,当点G在点E的左侧,且α= 58°时,求β的值;
②在点G的运动过程中,α和β之间有怎样的数量关系? 请写出你的猜想,并说明理由.

答案：
解:
(1)AB // CD，理由如下:
因为FM平分∠EFD，
所以∠EFM = ∠DFM.
因为∠EFM = ∠EMF，
所以∠DFM = ∠EMF，
所以AB // CD.
(2)①因为FH平分∠EFG，FM平分∠EFD，
所以设∠EFH = ∠GFH = φ，∠EFM = ∠DFM = θ，
则∠EFG = 2φ，∠EFD = 2θ，
所以∠GFD = ∠EFG + ∠EFD = 2φ + 2θ，∠HFM = ∠EFH + ∠EFM = φ + θ.
因为AB // CD，HN // FM，∠FHN = α，∠FGE = β，
所以∠GFN = ∠FGE = β，∠HFM = ∠FHN = α，
所以φ + θ = α.
因为∠GFN + ∠GFD = 180°，
所以β + 2φ + 2θ = 180°，
所以β + 2α = 180°，
即β = 180° - 2α，
当α = 58°时，β = 180° - 2α = 180° - 2×58° = 64°.
②当点G在运动过程中，α和β之间的数量关系是β = 180° - 2α或β = 2α，理由如下:
当点G在点E的左侧时，
由
(2)①可知β = 180° - 2α;
当点G在点E的右侧时，如答图所示，
因为FH平分∠EFG，
所以设∠EFH = ∠GFH = φ，
则∠EFG = 2φ，
设∠GFM = θ，则∠EFM = ∠EFG + ∠GFM = 2φ + θ，
所以∠HFM = ∠GFH + ∠GFM = φ + θ.
因为FM平分∠EFD，
所以∠EFM = ∠DFM = 2φ + θ，
所以∠DFG = ∠DFM + ∠GFM = 2φ + θ + θ = 2φ + 2θ.
因为AB // CD，HN // FM，
所以∠DFG = ∠FGE = β，∠HFM = ∠FHN = α，
所以2φ + 2θ = β，φ + θ = α，
所以β = 2α，
综上所述，α和β之间的数量关系是β = 180° - 2α或β = 2α.